Andrej Karpathy’s post “The Unreasonable Effectiveness of Recurrent Neural Networks” made splashes last year. The basic premise is that you can create a recurrent neural network to learn language features character-by-character. But is the resultant model any different from a Markov chain built for the same purpose? I implemented a character-by-character Markov chain in R to find out.

Source: @shakespeare
First, let’s play a variation of the Imitation Game with generated text from Karpathy’s tinyshakespeare dataset. Which snippets are from the RNN and which are from the Markov chain? Note that Karpathy’s examples are from the complete works, whereas my Markov chain is from tinyshakespeare (about 1/4 the size) because I’m lazy.
DUKE VINCENTIO:Well, your wit is in the care of side and that.
FRIAR LAURENCE:Or walk liest;
And the ears.
And hell!
In self.
PETRUCHIO:Persuading to our the enemy, even woman, I'll afford show'd and speaking of
England all out what least. Be satisfied! Now, sir.
Second Lord:They would be ruled after this chamber, and
my fair nues begun out of the fact, to be conveyed,
Whose noble souls I'll have the heart of the wars.
If you can’t tell, don’t be hard on yourself. The humble Markov chain appears to be just as effective as the state-of-the-art RNN at learning to spell (olde) English words. How can this be? Let’s think about how each of these systems work. Both are taking a sequence of characters and attempting to “predict” the next character in the sequence. The RNN does this by adjusting weight vectors to get an output vector that fits the specified response. The hidden layer maintains state over the training set. In the end, there is a confidence value attributed to each possible output character, which is used to predict the next character.
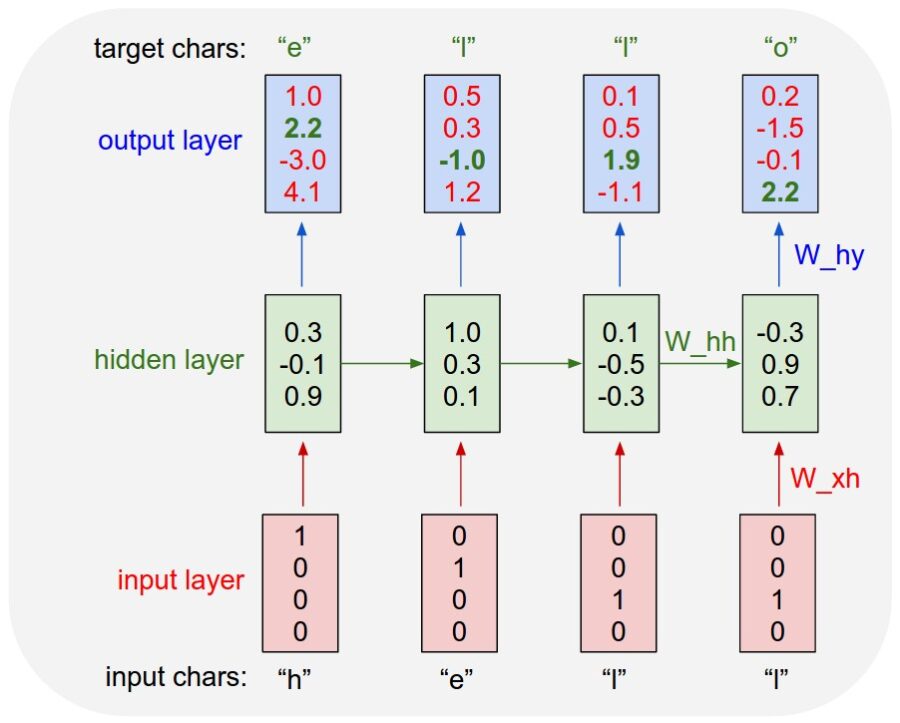
Source: Andrej Karpathy
On the other hand, training a Markov chain simply constructs a probability mass function incrementally across the possible next states. What this means is that the resulting pmf is not so different from the RNN output of confidences. Here’s an example of the pmf associated with the string ‘walk ‘:
> table(chain[['walk ']]) / length(chain[['walk ']]) a b i l m o u
0.4 0.1 0.1 0.1 0.1 0.1 0.1
This tells us that 40% of the time, the letter ‘a’ follows the sequence ‘walk ‘. When producing text, we can either treat this as the predicted value, or use the pmf to dictate the sampling. I chose the latter since it’s more interesting.
But how is state captured in the Markov chain since by definition a Markov chain is stateless? Simple: we use a character sequence as the input instead of a single character. For this post, I used a sequence of length 5, so the Markov chain is picking a next state based on the previous five states. Is this cheating or is this what the RNN is doing with hidden layers?
While the mechanics of RNNs differ significantly from Markov chains, the underlying concepts are remarkably similar. RNNs and deep learning might be the cool kids on the block, but don’t overlook what’s simple. You can get a lot of mileage from simple models, which have generally stood the test of time, are well understood, and easy to explain.
NB: I didn’t use a package to train and run the Markov chain, since it’s less than 20 LOC overall. A version of this code will appear in a forthcoming chapter of my book.
Brian Lee Yung Rowe is Founder and Chief Pez Head of Pez.AI // Zato Novo, a conversational AI platform for guided data analysis and automated customer service. Learn more at Pez.AI.
