Essentially good hypotheses lead decision-makers like you to new and better ways to achieve your business goals. When you need to make decisions such as how much you should spend on advertising or what effect a price increase will have your customer base, it’s easy to make wild assumptions or get lost in analysis paralysis. A business hypothesis solves this problem, because, at the start, it’s based on some foundational information. In all of science, hypotheses are grounded in theory. Theory tells you what you can generally expect from a certain line of inquiry. A hypothesis based on years of business research in a particular area, then, helps you focus, define and appropriately direct your research. You won’t go on a wild goose chase to prove or disprove it. A hypothesis predicts the relationship between two variables. If you want to study pricing and customer loyalty, you won’t waste your time and resources studying tangential areas.
Data collection establishes the foundation for appraising quality of a product or service. But without correct data processing, it becomes challenging to make an objective conclusion. Sometimes, the observation is wrongly interpreted
Hypothesis testing is the process of using statistics to determine the probability that a specific hypothesis is true. it’s is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.
Hypothesis testing is categorized as parametric test and nonparametric test. The parametric test includes z-test, t-test, f-test. The nonparametric test includes sign test, Wilcoxon Rank-sum test, Kruskal-Wallis test and permutation test.
Application of Parametric Test:
This test is used for testing the population mean when the population standard deviation is known and the population under study is normal or non-normal for the large sample. But when the sample size is small, we apply the Z-test only when the population under study is normal. However if sample size is less than 30 then use t-test for testing the population mean when the population standard deviation (σ) is unknown and the population under study is normal
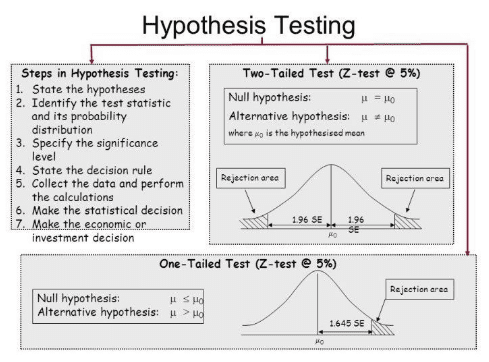
We first formulate the null hypothesis (H0) and alternative hypothesis (H1) and then calculate the value of the test statistics using the below formula:
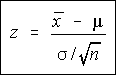
z-test
We obtain the critical(cut-off or tabulated) value(s) of the test statistics Z corresponding to the given level of significance(α)
Now take a decision about the null hypothesis as follows:
- Using the Critical region Approach — In this approach, compare the calculated value of the test statistics(z) with the critical value(s) obtained above
- Using p-value approach — Compare the calculated p-value with the given level of significance. if p-value is less than or equal to α, we reject the null hypothesis and if it is greater than α, we do not reject the null hypothesis.
So finally if null hypothesis is rejected, we conclude that the sample provides us sufficient evidence against the null hypothesis at α% level of significance.