“When I think back on all the crap I’ve learned in high school, It’s a wonder I can think at all” – Simon and Garfunkel, Kodachrome
Growing up in the ’60s in California, we were subjected to a lot of educational experiments. We had beanbag chairs in class. We squinted into uncomfortable metal and glass contraptions for “speed reading”. We read snippets of literature on coloured, laminated cards. I remember being proud of reaching SRA level ‘purple’, at the end of the reading crate, but not reading an actual book. The four food groups were replaced with a pyramid, encouraging you to eat lots and lots of carbs. And then there was “New Math.”

Figure 2: Why Johnny can’t read. A tachistoscopic projector and the SRA reading system
New math was an ambitious change in the mathematics curriculum in response to the “Sputnik Shock.” It was a Big Deal in the US, and to a lesser extent, Europe. It was a bold and ambitious plan to turn every child into the next Werner von Braun (assuming Werner von Braun was Alan Turing). It was also a demonstrable failure.
I liked it. Well, not all of it. If you are like me, you were so immersed in it, you can’t reliably distinguish it from old math (e.g., multiplication tables, algebra, geometry, etc.). New Math expanded (and displaced) traditional mathematics curricula with abstract topics, such as set theory, modular arithmetic, algebraic inequalities, number bases, symbolic logic, and Boolean algebra. Whew! Who out there remembers inequalities? (hint: it involves number lines and shading in objects)
It is a bit too easy to be cynical and debate which topic was the most useless, and New Math was quite rightly criticized at the time.
New Math died in 1973. (The murderers will be revealed later.) After nearly 5 decades, I wanted to understand what it was all about. What follows is a first-hand account of my experience. Many of you will feel my pain. Perhaps, like me, you will have had experienced déjà vu in college or graduate school, where some of these concepts re-appeared and even started to make sense.
Base Numbers
The most ridiculed topic was base numbers. Tom Lehrer parodized it in verse, which captures the confusion of parents and teachers alike:
The book that I got this problem out of wants you to do it in base eight. But don’t panic! Base eight is just like base ten really — if you’re missing two fingers!
Shall we have a go at it? Hang on…
You can’t take three from two,
Two is less than three,
So you look at the four in the eights place.
Now that’s really four eights,
So you make it three eights,
Regroup, and you change an eight to eight ones
And you add ’em to the two,
And you get one-two base eight,
Which is ten base ten,
And you take away three, that’s seven.
Ok?
Hooray for New Math,
It’s so simple,
So very simple,
That only a child can do it!”
Arguably, base numbers were the most accessible and the most practical of the lot. As a quick refresh, here is 7 in base 2:
7 = 2⁰+2¹+2² = 111 base 2
Addition (and other arithmetic operations) are performed as in base 10:
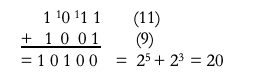
Clearly, binary mathematics was to become critical in the digital age. We had a school assembly with a NASA engineer and a ten-foot high computer to emphasize this point. Who didn’t want to be an astronaut? When will we all have computers of our own?
Learning base numerals and other alternate number systems is valuable in the same way learning foreign language helps you understand your primary language. An analogy from the biology: “If you want to know why there are only two sexes, try to imagine the evolutionary advantages of 3… or 7.”
Binary is unique, in that it is the natural language of switches (on/off), logic (True/False), and of course, computers. Binary math and its’ twin, Boolean algebra, allows us to design circuits to perform any mathematical calculation (Figure 3).
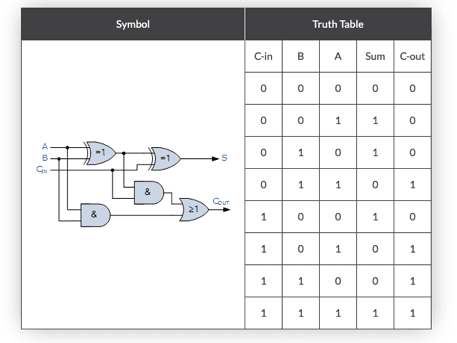
Figure 3: A physical embodiment of an adding machine, combining elementary logic circuits AND, OR, and NOT. The variable C_out is the carry digit. Cool, huh?
We learned that a computer could do anything mathematical. Boolean algebra could be used to solve logic and propositional calculus. Computers could perform anything in mathematics or logical reasoning better than humans! (Actually, that was a bit depressing.) A new, trendy, thing “Artificial Intelligence” was all the rage. Movies had apocalyptic warnings about computers ruling the world (2001 [1968], Collosus: The Forbin Project [1970]). Sound familiar?
So, us snot-nosed children understood something our parents didn’t. We were only a few weeks away from understanding how a digital computer works. Boolean algebra was getting somewhere, but suddenly, we shifted gears into to another level of abstraction. It was 5th grade and time for some new algebras.
Set Theory
Fourth and fifth grade math is a bit of a blur to me. For some reason, we were no longer to think about numbers as quantities, but numbers as things, and things belonged to sets. From what I remember, an integer between 4 and 8 became “the set of integers:”
S0 = {5, 6, 7}, which was the intersection of two infinite sets:
S0 = S1 ⋂ S2, where
S1 = {-∞, … 4, 5, 6, 7} and S2 = {5, 6, 7, 8, 9 , … ∞}
It was a complete mystery to me then and now, why math was supposed to get easier by thinking of numbers as ‘objects’ in ‘sets’. If that labels me a philistine, consider I was one of the petit bourgeois. What did the proletarians make of all this?
Set Theory is potentially foundational to many branches of mathematics, as axioms in several fields can all be cast into the more general theory. On the other hand, it is clumsy and tedious in practice, and the native methods of each discipline are simpler and easier to work with. One unfortunate legacy of set theory is the Venn Diagram, which about the only thing anyone remembers — and is ubiquitously used in business presentations, to give the illusion of content.
Algebraic Inequalities
Since it is rather difficult to think of sets of continuous numbers, our teachers simultaneously introduced the algebraic inequalities to deal with quantities on real number lines, so a real number between 4 and 8 would be represented by
4 < x < 8
Which could be expressed using the logical/Boolean notation:
x > 4 AND x <8
Problems moved on to thinking in two dimensions (4x+y < 0), so we were finally moving into traditional algebra. Set theory was cast aside, perhaps because they had run out of examples of problems easily solved with set theory.
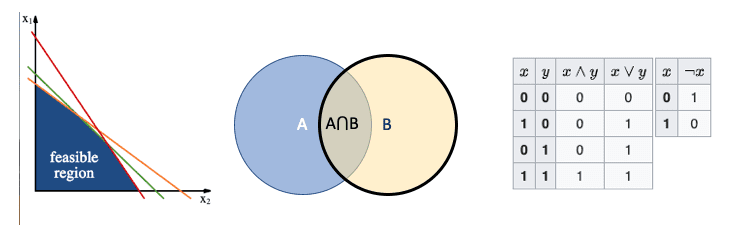
Figure 4: One Algebra to rule them all? Parsing Space, Things, and Propositions.
By the end of the 5th grade, our minds whirled with the nuances of the operations union(U), addition(+), and ‘logical AND’(⋀). They were all “kind of” the same idea, but the math was different in each case. So far, we had been introduced to three algebras, before mastering basic algebra. Obviously, what was needed was another algebra.
Modular Arithmetic
I was spared investing too much time on Modular Arithmetic — probably because my teachers did not know what it is good for. To be clear: my teachers in were mostly laid off rocket scientists. (In case you missed it, we won the space race in 1969.) If my teachers didn’t see the point, they were probably on to something.
Modular arithmetic (sometimes called clock arithmetic) deals with numbers that repeat around a cycle — or modulus (in the case of clocks, 12), and finding the remainder. Two numbers, a and b, are said to be congruent if they have the same remainder when divided by n.
a ≡ b mod n
In clock time, 100 hours from midnight is congruent to 4 AM
4 ≡ 100 mod 12
In Western music, frequencies double every twelve notes, so all “C-notes” are congruent in mod 12.
There are rules for addition, subtraction, division, commutation, etc., analogous to the rules of normal arithmetic. But, while binary math is a little bit different than base 10 math, modular math is A LOT different.
I have been a professional scientist for 30 years and have never used the “MOD” button on my calculator, so whoever thought the button would be useful must have been a real devotee. On the other hand, maybe he was showing off he knew what a modulus was and no one in the design meeting had the guts to ask.
I had not thought about it for decades, until I sat in on a fascinating lecture about its’ inventor, Carl Friedrich Gauss, on his work developing Number Theory [3]. It is only briefly summarized below, so as to not scare you. Reader advisory: this will hurt a bit.
The Golden Theorem (Quadratic Reciprocity Theorem)
It turns out that all primes can be divided into two families, those congruent to 1 mod 4 and those congruent to 3 mod 4.
Family 1
5 13 17 29 37 41 53 61 73 79 89 97 101…
Family 2
3 7 11 19 23 31 43 47 59 67 71 83 103 …
Primes in the first series can be square roots of each other, at least in modular mathematics. (If p is the modular square root of q, then q is the modular square root of p). For example, 13 and 29 are have ‘reciprocal modular residues’
29 ≡ 16 mod 13 ≡ 4² mod 13
13 ≡ 100 mod 29 ≡ 10² mod 29
This is what I meant by “a lot different.” This kind of thing just doesn’t happen in normal math. It takes dedication to appreciate what this means, and its’ significance eludes most of us. This much I do know — this is such an important result that there have been 246 published proofs, six by Gauss himself [2]. It was critical to finding solutions to problems (such as factoring huge polynomials) that could never practically be solved by brute force. It is also the foundation for proving Fermat’s Last Theorem, which given the level of abstraction, it is not surprising took 300 years to do.
A prominent application of modular math is cryptography (the familiar RSA token uses a very simple modular algorithm to encrypt and decrypt messages). This begs the question of what were us juvenile delinquents supposed to have gained from studying this?
Mathematics is full of weird and wonderful things like this, but few people would voluntarily enroll in a course on Mathematics Appreciation. If you’d like to know more, I recommend the Gresham College lecture by Raymond Flood on YouTube[3].
Still not interested? OK. Let’s try something more age appropriate.
Arithmetic in Egyptian and Roman Numerals
At a recent technical conference, I noticed that none of the younger attendees could read the date on the façade of the lecture hall. This made me sad. So here is a brief rehash on how to do math with Roman numerals. Again, not that anyone needs to know this, but it is kind of fun.
Rules for Addition in Roman numerals
1. Eliminate subtractive notation (e.g. replace IV with IIII)
2. Group all the symbols in order e.g. CCCLXXXVVIIIIIIII)
3. Simplify/contraction: Right to left, replace repeated symbols with their higher value equivalents (e.g. VV →X). Egyptian is more annoying as they don’t have 5’s, 50’s and so on, so there are more symbols to count.
4. Reintroduce subtractive notation (if you feel like it)
Multiplication is possibly easier than with Arabic numbers:
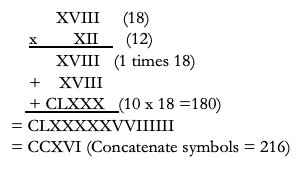
A few more fun facts: the Romans invented their own version of the abacus (Figure 1), to speed such calculations. Doing long division or decimals in Roman numbers is painful, yet up until the eighteenth century, Roman numerals were still used for bookkeeping.
Math shouldn’t hurt. To me, it has always been interesting. But that is just me.
Post Mortem:
In 1973 David McCall, an advertising executive, frustrated at helping his child learn multiplication tables, created the Saturday morning cartoon series, “Multiplication Rock,” for ABC television. This was the most iconic manifestation of the “back to basics” movement. Early backers were none other than Michael Eisner and Chuck Jones. God bless Chuck Jones.
Historian/mathematician, Morris Kline, offered this succinct critic of New Math: “[A]bstraction is not the first stage, but the last stage, in a mathematical development.” Understanding the structure and theory of mathematics is not really necessary for its’ use, but some of us become curious. Many of the things we learned are no longer taught, and math is very dry and boring again, like in the old days. Some that has been dropped is the most fun.
I subjected my poor daughter New Math when she was very young (But not set theory!). She liked it. She picked up binary math in only a few hours. So, I started guest lecturing at her traditional, Scottish, girls-only primary school. They liked it. The girls jumped to the blackboards, to add to the list of numerals in Japanese, Indian, Chinese, as well as alternative methods for multiplying numbers. The teachers started attending my lectures. To my surprise, they had not learned how to work with Roman numbers. They all probably liked it more knowing they were not going to be graded on this trivia; I just wanted them to know it’s there.
Russell Anderson did not become an astronaut, but he did work on the Space Station and “Star Wars” missile defence at McDonnell Douglas Astronautics in 1984. He went on to complete a Ph.D. in Bioengineering from the University of California. His academic research involved learning in biological systems (neural, immune, and evolutionary). He has served as Chief Scientist at IBM, KPMG, Opera Solutions, NICE/Actimize, HCL, HNC Software, Mastercard, JP Morgan Chase, and Halifax Bank of Scotland. He has authored over 30 scientific publications and 8 patents.
Questions/Comments are welcome: [email protected]
[1] Tom Lehrer, New Math Song (1965). https://www.youtube.com/watch?v=UIKGV2cTgqA
[2] 246 proofs of Quadratic Reciprocity Theorem. http://www.rzuser.uni-heidelberg.de/~hb3/fchrono.html
[3] Raymond Flood. Gauss and Germain. Gresham Lecture Series on Great Mathematicians. February 2016 https://www.gresham.ac.uk/lectures-and-events/gauss-and-germain#p7i…
[4] Morris Kline(1973). Why Johnny Can’t Add: The Failure of the New Math. New York: St. Martin’s Press.
Originally posted here
