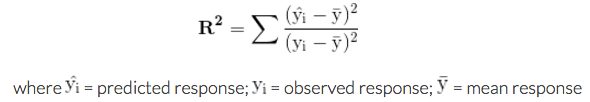One of most excruciating pain points during Data Exploration and Preparation stage of an Analytics project are missing values.
How do you deal with missing values – ignore or treat them? The answer would depend on the percentage of those missing values in the dataset, the variables affected by missing values, whether those missing values are a part of dependent or the independent variables, etc. Missing Value treatment becomes important since the data insights or the performance of your predictive model could be impacted if the missing values are not appropriately handled.
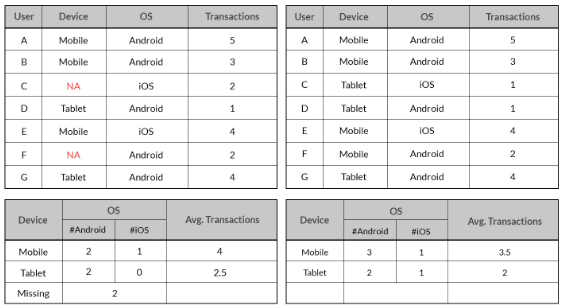
The 2 tables above give different insights. The inference from the table on the left with the missing data indicates lower count for Android Mobile users and iOS Tablet users and higher Average Transaction Value compared to the inference from the right table with no missing data. The inference from the data with missing values could adversely impact business decisions. The best scenario is to get the actual value that was missing by going back to the Data Extraction & Collection stage and correcting possible errors during these stages. Generally, that won’t be the case and you will still be left with missing values.
Techniques
Let’s look at some techniques to treat the missing values:
I. Deletion
Unless the nature of missing data is ‘Missing completely at random’, the best avoidable method in many cases is deletion.
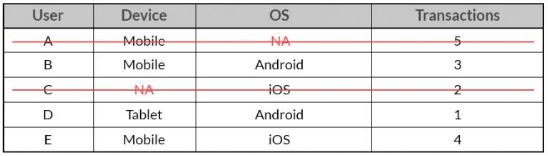
a. Listwise: In this case, rows containing missing variables are deleted.
In the above case, the entire observation for User A and User C will be ignored for listwise deletion
b. Pairwise: In this case, only the missing observations are ignored and analysis is done on variables present.
In the above case, 2 separate sample data will be analyzed, one with the combination of User, Device and Transaction and the other with the combination of User, OS and Transaction. In such a case, one won’t be deleting any observation. Each of the samples will ignore the variable which has the missing value in it.
Both the above methods suffer from loss of information. Listwise deletion suffers the maximum information loss compared to Pairwise deletion. But, the problem with pairwise deletion is that even though it takes the available cases, one can’t compare analyses because the sample is different every time.
II. Imputation
a. Popular Averaging Techniques
Mean, median and mode are the most popular averaging techniques, which are used to infer missing values. Approaches ranging from global average for the variable to averages based on groups are usually considered.
For example: if you are inferring missing value for Revenue, you might assign the average defined by mean, median or mode to such missing value. You could also consider taking into account some other variables such as Gender of the User and/or the Device OS to calculate such an average to be assigned to the missing values.
Though you can get a quick estimate of the missing values, you are artificially reducing the variation in the dataset as the missing observations could have the same value. This may impact the statistical analysis of the dataset since depending on the percentage of missing observations imputed, metrics such as mean, median, correlation, etc may get affected.
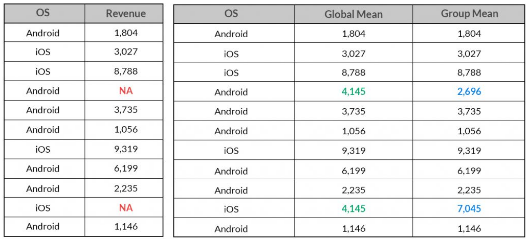
The above table shows the difference in imputed missing values of Revenue arrived by taking its global mean and mean based on which OS platform it belongs to.
b. Predictive Techniques
Imputation of missing values from predictive techniques assumes that the nature of such missing observations are not observed completely at random and the variables chosen to impute such missing observations have some relationship with it, else it could yield imprecise estimates.
In the examples discussed earlier, a predictive model could be used to impute the missing values for Device, OS, Revenues. There are various statistical methods like regression techniques, machine learning methods like SVM and/or data mining methods to impute such missing values.
Illustration
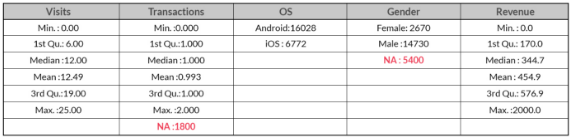
Let’s take a look at an example where we shall test all the techniques discussed above to infer or deal with such missing observations. With the information on Visits,Transactions, Operating System, and Gender, we need to build a model to predict Revenue. The summary of the information is given below:
We have a total of 7200 missing data points (Transactions: 1800, Gender: 5400) out of 22,800 observations. Almost 8% and 24% data points are missing for ‘Transactions’ and ‘Gender’ respectively.
Revenue Prediction
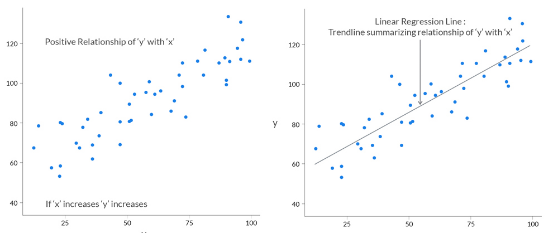
We will be using a linear regression model to predict ‘Revenue’. A quick intuitive recap of Linear Regression Assume ‘y’ depends on ‘x’. We can explore their relationship graphically as below:
Missing Value Treatment
Let’s now deal with the missing data using techniques mentioned below and then predict ‘Revenue’.
A. Deletion
Steps Involved:
i) Delete
Delete or ignore the observations that are missing and build the predictive model on the remaining data. In the above example, we shall ignore the missing observations totalling 7200 data points for the 2 variables i.e. ‘Transactions’ and ‘Gender’.
ii) Impute ‘Revenue’ by Linear Regression
Build a Linear model to predict ‘Revenue’ with 15,600 observations.
B. Impute by Average
Steps Involved:
i) Impute ‘Transactions’ by Mean
We shall impute the missing data points for ‘Transactions’ variable by looking at the group means of ‘Transactions’ by ‘OS’.
Mean of Transactions for Users on Android: 0.74
Mean of Transactions for Users on iOS: 1.54
All the missing observations for ‘Transactions’ will get 0.74 and 1.54 as its value for Users on Android and iOS respectively.
ii) Impute ‘Gender’ by Mode
Since ‘Gender’ is a categorical variable, we shall use Mode to impute the missing variables. In the given dataset, the Mode for the variable ‘Gender’ is ‘Male’ since it’s frequency is the highest. All the missing data points for ‘Gender’ will be labeled as ‘Male’.
iii) Impute ‘Revenue’ by Linear Regression
Build a Linear model to predict ‘Revenue’ with the entire dataset totalling 22,800 observations.
C. Impute by Predictive Model
Steps Involved:
i) Impute ‘Gender’ by Decision Tree
There are several predictive techniques; statistical and machine learning to impute missing values. We will be using Decision Trees to impute the missing values of ‘Gender’. The variables used to impute it are ‘Visits’, ‘OS’ and ‘Transactions’.
ii) Impute ‘Transactions’ by Linear Regression
Using a simple linear regression, we will impute ‘Transactions’ by including the imputed missing values for ‘Gender’ (imputed from Decision Tree). The variables used to impute it are ‘Visits’, ‘OS’ and ‘Gender’.
iii) Impute ‘Revenue’ by Linear Regression
Build a Linear model to predict ‘Revenue’ with the entire dataset totalling 22,800 observations.
Linear Regression Model Evaluation
A common and quick way to evaluate how well a linear regression model fits the data is the coefficient of determination or R2.
- R2 indicates the sensitivity of the predicted response variable with the observed response or dependent variable (Movement of Predicted with Observed).
- The range of R2 is between 0 and 1.
R2 will remain constant or keep on increasing as long as you add more independent variables to your model. This might result in overfitting. Overfitting leads to good fit on the data used to build the model or in-sample data but may poorly fit out-of-sample or new data. Adjusted R2 overcomes this shortcoming of R2 to a great extent. Adjusted R2 is a modified version of R2 that has been adjusted for the number of predictors in the model.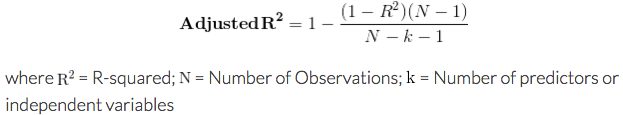
- The Adjusted R2 will penalize R2 for keeping on adding independent variables (k in the equation) that do not fit the model.
- Adjusted R2 is not guaranteed to increase or remain constant but may decrease as you add more and more independent variables.
Model Comparison post-treatment of Missing Values
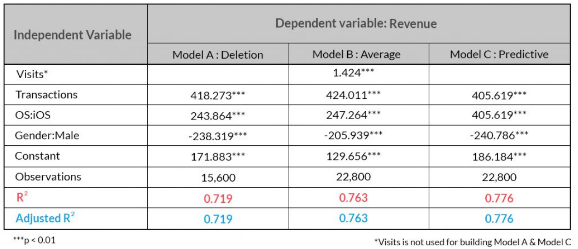
Let’s compare the linear regression output after imputing missing values from the methods discussed above:
In the above table, the Adjusted R2 is same as R2 since the variables that do not contribute to the fit of the model haven’t been taken into consideration to build the final model.
Inference:
- It can be observed that ‘Deletion’ is the worst performing method and the best one is ‘Imputation by Predictive Model’ followed by ‘Imputation by Average’.
- ‘Imputation by Predictive Model’ delivers a better performance since it not only delivers a higher Adjusted R2 but also requires one independent variable (‘Visits’) less to predict ‘Revenue’ compared to ‘Imputation by Average’.
Conclusion
Imputation of missing values is a tricky subject and unless the missing data is not observed completely at random, imputing such missing values by a Predictive Model is highly desirable since it can lead to better insights and overall increase in performance of your predictive models.
Source Code and Dataset to reproduce the above illustration available here
This blog originally appeared here.