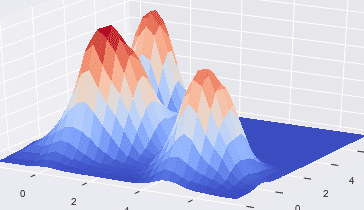
Data scientists and predictive modelers often use 1-D and 2-D aggregate statistics for exploratory analysis, data cleaning, and feature creation. Higher dimensional aggregations, i.e., 3 dimensional and above, are more difficult to visualize and understand. High density regions are one example of these N-dimensional statistics. High density regions can be useful for summarizing common characteristics across multiple variables. Another use case is to validate a forecast prediction’s plausibility by exploring the densities associated with the forecast. Other machine learning approaches such as clustering and kernel density estimation are similar to finding high density regions, but these methods are different in a few important ways. It is worth noting why these methods, while useful, are not design exactly designed for the purpose of finding these regions. The goal is to use KernelML to efficiently find the regions of highest density for an N-dimensional dataset.
My approach to developing this algorithm was to find a set of, common sense, constraints to construct the loss metric.
The high density region estimator, HDRE, algorithm uses N multivariate uniform distributions to cluster the data. Uniform distributions are less sensitive to outliers than normal distributions, and these distribution truncate low correlation across the vertical and horizontal axes while keeping high correlations along the diagonal axes. The clusters are constrained to shared variance across all clusters and equal variance across all dimensions. The data should be normalized to allow the clusters to scale properly across each dimension.
See more here.