I was in the process of computing some definite integrals involving special mathematical constants, when I discovered WolframAlpha. It solves tons of mathematical problems, for free, online, offering exact solutions whenever possible. Not just integrals, but matrix computations and much more.
In my case, I was trying to see, if by computing an integral in two different ways, one using the original function on the original domain, and the other one using the inverse function on the image domain, I would be able to find a mathematical equality involving one special mathematical constant for the first integral (say e or Pi) and one involving some other special mathematical constants (say log 2) for the second integral. The idea being that, if I manage to find such a relationship, then it means that the two mathematical constants (say e and log 2) are a simple function of each other, and thus we only need one.
Needless to say, I was not able to find such relationships. I did find some interesting stuff though. First, the WolframAlpha API, and then, I rediscovered an obscure but fundamental theorem, not mentioned in math textbooks — a theorem linking the integral of a function to the integral of its inverse.
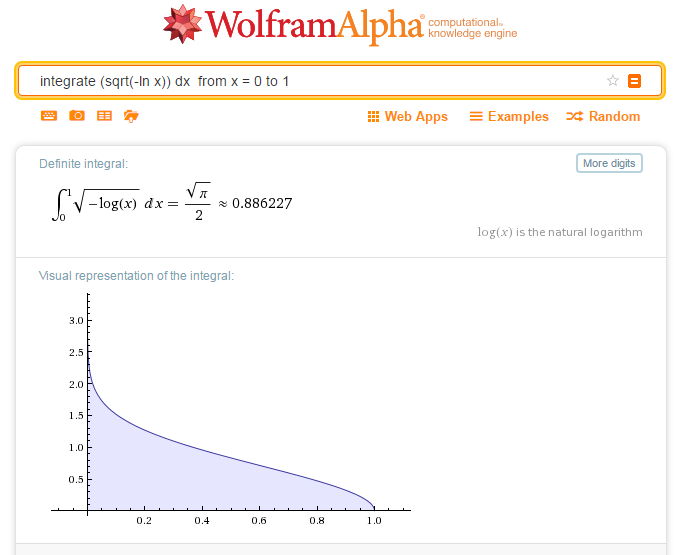
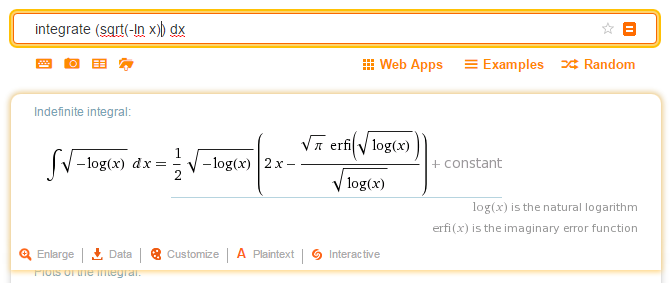
Below is the results of using the API for the inverse of f(x) = exp(- x^2) between 0 and infinity: a famous integral involving the square root of Pi. The inverse is g(x) = SQRT(- log x) between 0 and 1: both integrals, for symmetry reasons (based on the theorem in question), have the same value. WolframAlpha just confirmed this fact, rather than – as was my hope – getting a value based on special math constants other than Pi.
Note that Symbolab offers a similar API. In the process, I also discovered HostMath, to write math formulas online (a math editor) then take screenshots and include the math formulas as images in an HTML document. I used it for the first time in this article.