This article on going deeper into regression analysis with assumptions, plots & solutions, was posted by Manish Saraswat. Manish who works in marketing and Data Science at Analytics Vidhya believes that education can change this world. R, Data Science and Machine Learning keep him busy.
Regression analysis marks the first step in predictive modeling. No doubt, it’s fairly easy to implement. Neither it’s syntax nor its parameters create any kind of confusion. But, merely running just one line of code, doesn’t solve the purpose. Neither just looking at R² or MSE values. Regression tells much more than that!
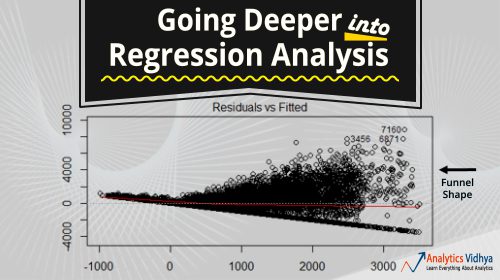
In R, regression analysis return 4 plots using plot(model_name) function. Each of the plot provides significant information or rather an interesting story about the data. Sadly, many of the beginners either fail to decipher the information or don’t care about what these plots say. Once you understand these plots, you’d be able to bring significant improvement in your regression model.
For model improvement, you also need to understand regression assumptions and ways to fix them when they get violated.
In this article, I’ve explained the important regression assumptions and plots (with fixes and solutions) to help you understand the regression concept in further detail. As said above, with this knowledge you can bring drastic improvements in your models.
What you can find in this article :
Assumptions in Regression
What if these assumptions get violated ?
- Linear and Additive
- Autocorrelation
- Multicollinearity
- Heteroskedasticity
- Normal Distribution of error terms
Interpretation of Regression Plots
- Residual vs Fitted Values
- Normal Q-Q Plot
- Scale Location Plot
- Residuals vs Leverage Plot
You can find the full article here. For other articles about regression analysis, click here.
Note from the Editor: For a robust regression that will work even if all these model assumptions are violated, click here. It is simple (it can be implemented in Excel and it is model-free), efficient and very comparable to the standard regression (when the model assumptions are not violated). And if you need confidence intervals for the predicted values, you can use the simple model-free confidence intervals (CI) described here. These CIs are equivalent to those being taught in statistical courses, but you don’t need to know stats to understand how they work, and to use them. Finally, to measure goodness-of-fit, instead of R-Squared or MSE, you can use this metric, which is more robust against outliers.
DSC Resources
- Career: Training | Books | Cheat Sheet | Apprenticeship | Certification | Salary Surveys | Jobs
- Knowledge: Research | Competitions | Webinars | Our Book | Members Only | Search DSC
- Buzz: Business News | Announcements | Events | RSS Feeds
- Misc: Top Links | Code Snippets | External Resources | Best Blogs | Subscribe | For Bloggers
Additional Reading
- What statisticians think about data scientists
- Data Science Compared to 16 Analytic Disciplines
- 10 types of data scientists
- 91 job interview questions for data scientists
- 50 Questions to Test True Data Science Knowledge
- 24 Uses of Statistical Modeling
- 21 data science systems used by Amazon to operate its business
- Top 20 Big Data Experts to Follow (Includes Scoring Algorithm)
- 5 Data Science Leaders Share their Predictions for 2016 and Beyond
- 50 Articles about Hadoop and Related Topics
- 10 Modern Statistical Concepts Discovered by Data Scientists
- Top data science keywords on DSC
- 4 easy steps to becoming a data scientist
- 22 tips for better data science
- How to detect spurious correlations, and how to find the real ones
- 17 short tutorials all data scientists should read (and practice)
- High versus low-level data science
Follow us on Twitter: @DataScienceCtrl | @AnalyticBridge