This is the 2nd part of the article on a few applications of Fourier Series in solving differential equations. All the problems are taken from the edx Course: MITx – 18.03Fx: Differential Equations Fourier Series and Partial Differential Equations. The article will be posted in two parts (two separate blongs)
We shall see how to solve the following ODEs / PDEs using Fourier series:
- Solve the PDE for Heat / Diffusion using Neumann / Dirichlet boundary conditions
- Solve Wave equation (PDE).
- Remove noise from an audio file with Fourier transform.
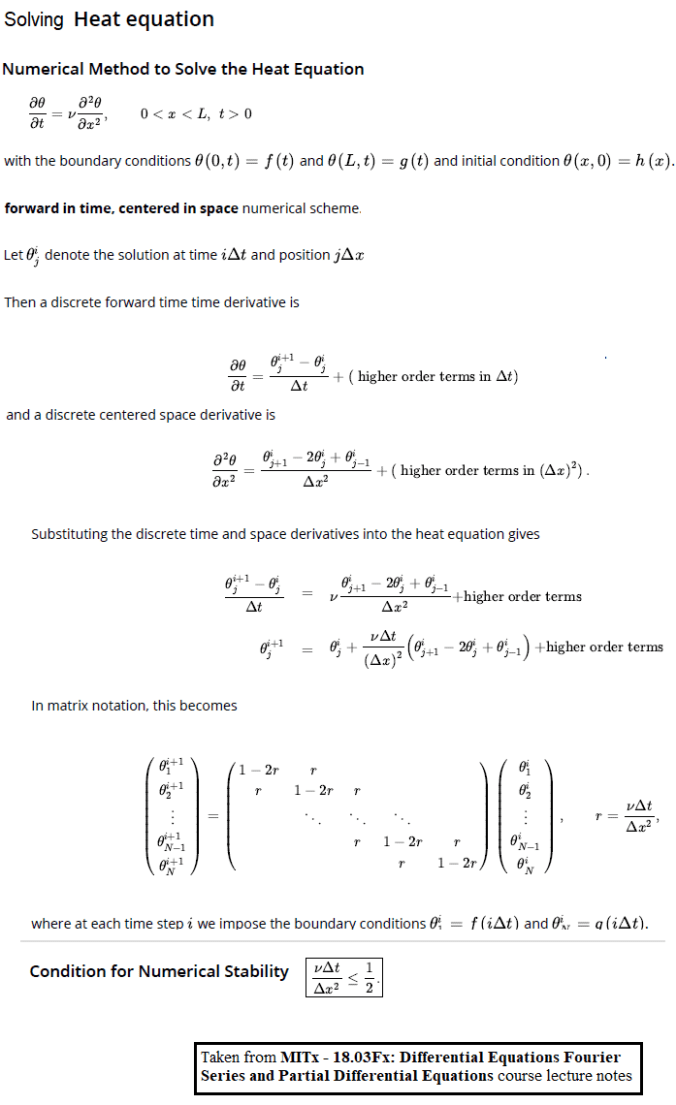
Heat / Diffusion Equation


The following animation shows how the temperature changes on the bar with time (considering only the first 100 terms for the Fourier series for the square wave).
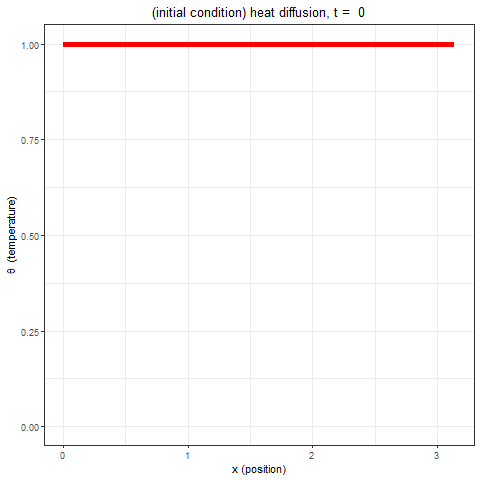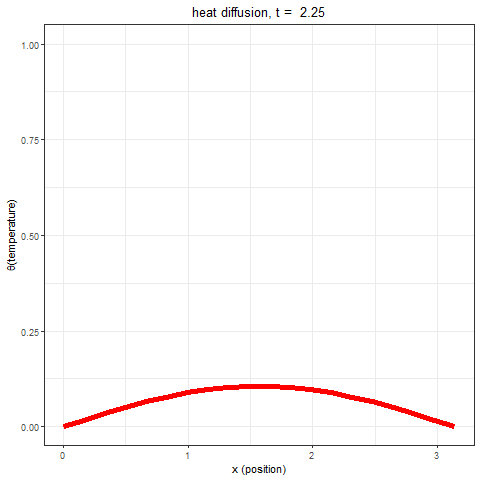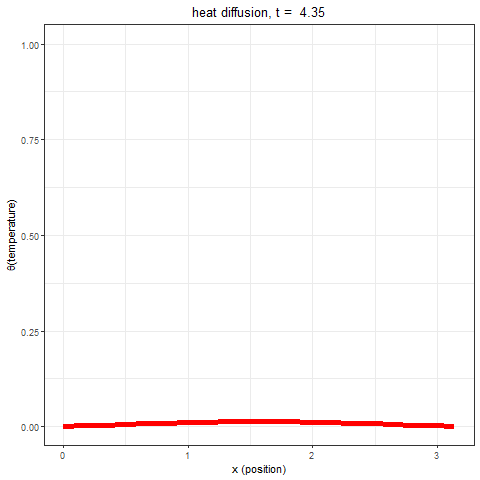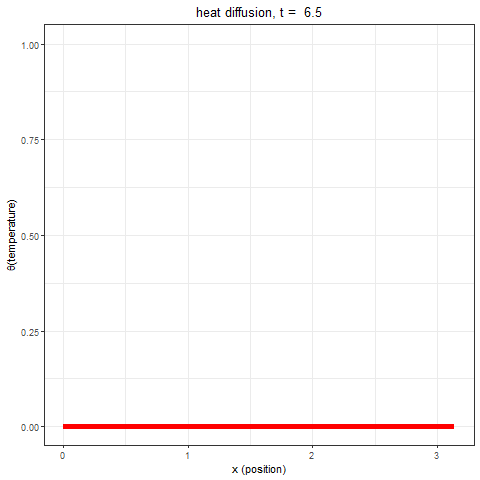
Let’s solve the below diffusion PDE with the given Neumann BCs.

As can be seen from above, the initial condition can be represented as a 2-periodic triangle wave function (using even periodic extension), i.e.,
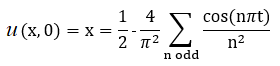
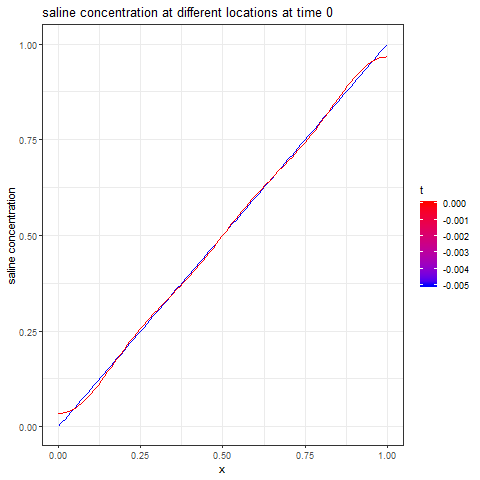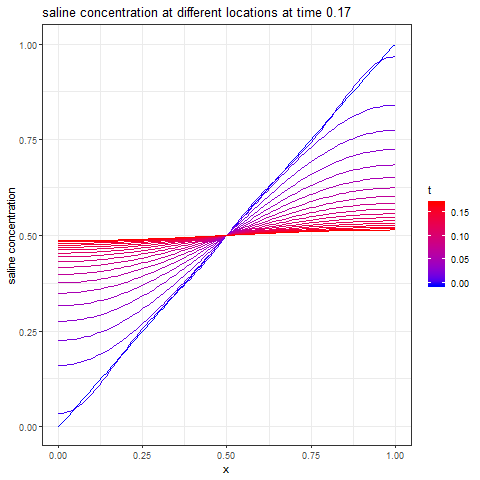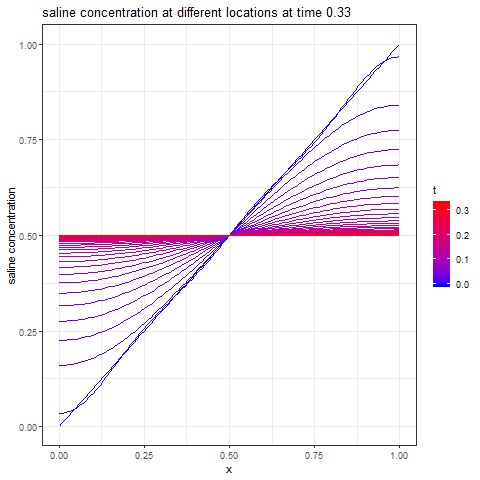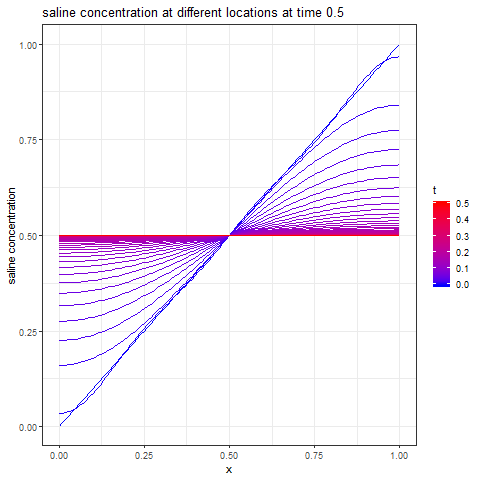
The next animation shows how the different points on the tube arrive at the steady-state solution over time.
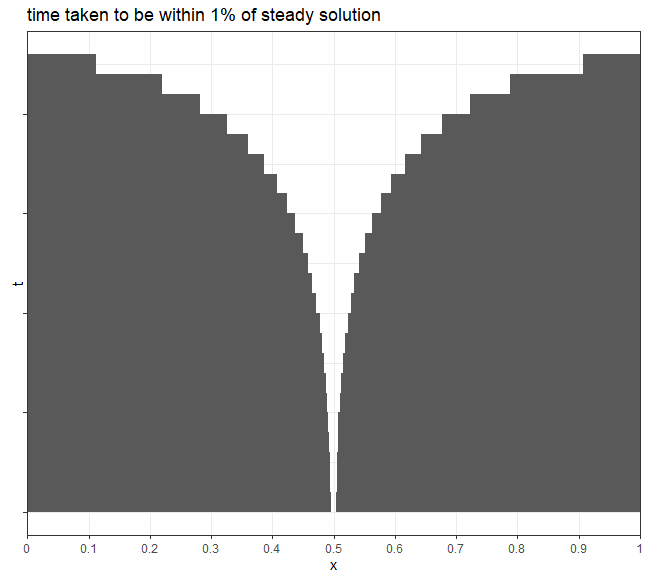
The next figure shows the time taken for each point inside the tube, to approach within 1% the steady-state solution.
with the following
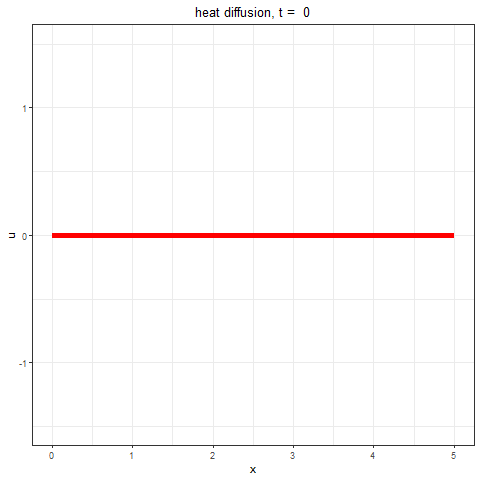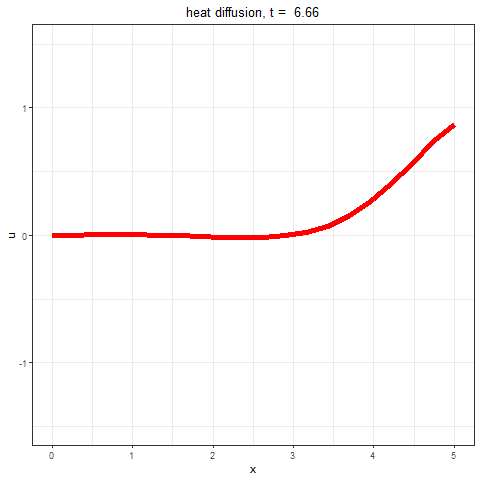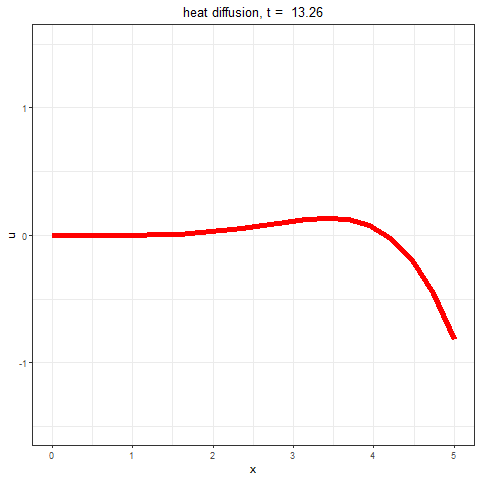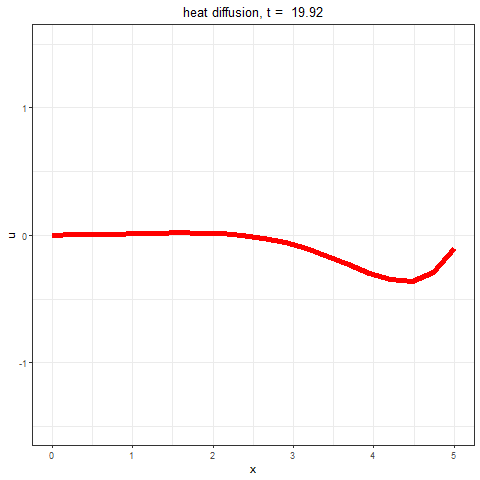
- L=5, the length of the bar is 5 units.
- Dirichlet BCs: u(0, t) =0, u(L,t) = sin(2πt/L), i.e., the left end of the bar is held at a constant temperature 0 degree (at ice bath) and the right end changes temperature in a sinusoidal manner.
- IC: u(x,0) = 0, i.e., the entire bar has temperature 0 degree.
The following R code implements the numerical method:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#Solve heat equation using forward time, centered space scheme#Define simulation parametersx = seq(0,5,5/19) #Spatial griddt = 0.06 #Time steptMax = 20 #Simulation timenu = 0.5 #Constant of proportionalityt = seq(0, tMax, dt) #Time vectorn = length(x)m = length(t)fLeft = function(t) 0 #Left boundary conditionfRight = function(t) sin(2*pi*t/5) #Right boundary conditionfInitial = function(x) matrix(rep(0,m*n), nrow=m) #Initial condition#Run simulationdx = x[2]-x[1]r = nu*dt/dx^2#Create tri-diagonal matrix A with entries 1-2r and r |
The tri-diagonal matrix A is shown in the following figure
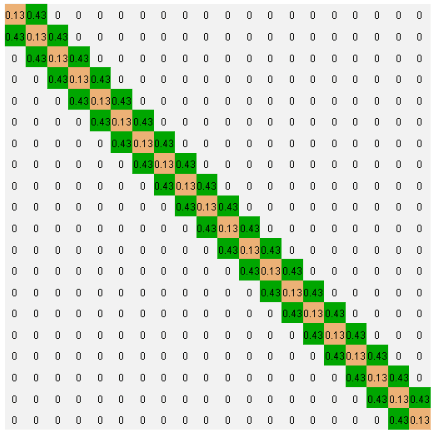
|
1
2
3
4
5
6
7
8
9
10
11
|
#Impose inital conditionsu = fInitial(x)u[1,1] = fLeft(0)u[1,n] = fRight(0)for (i in 1:(length(t)-1)) { u[i+1,] = A%*%(u[i,]) # Find solution at next time step u[i+1,1] = fLeft(t[i]) # Impose left B.C. u[i+1,n] = fRight(t[i]) # Impose right B.C.} |
The following animation shows the solution obtained to the heat equation using the numerical method (in R) described above,
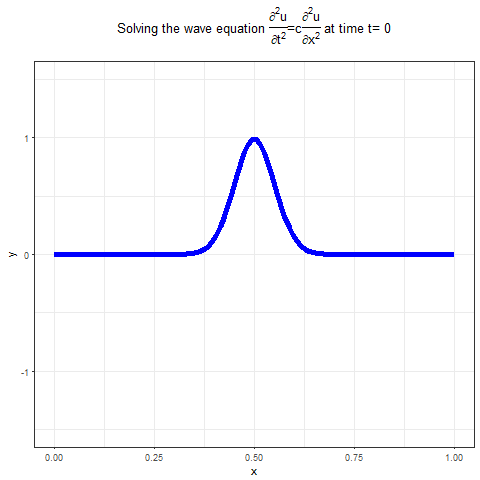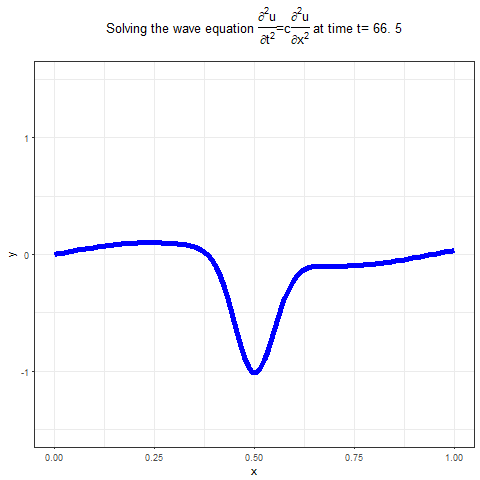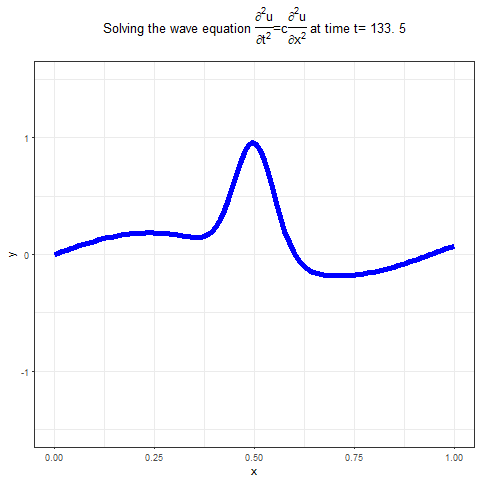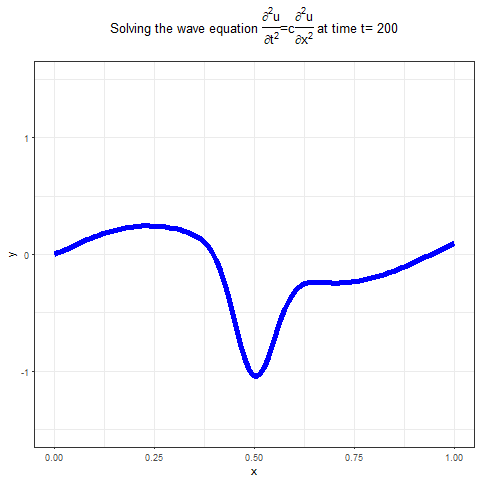
Wave Equation
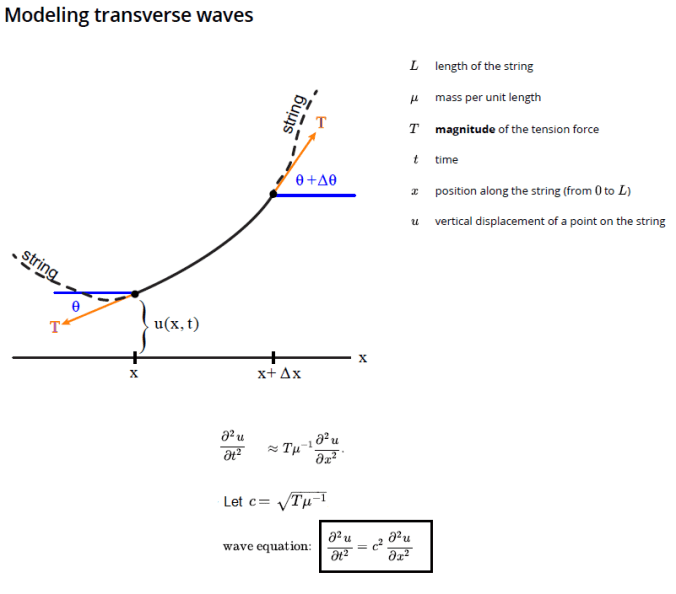

The next figure shows how can a numerical method be used to solve the wave PDE

Implementation in R
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#Define simulation parametersx = seq(0,1,1/99) #Spatial griddt = 0.5 #Time steptMax = 200 #Simulation timec = 0.015 #Wave speedfLeft = function(t) 0 #Left boundary conditionfRight = function(t) 0.1*sin(t/10) #Right boundary conditionfPosInitial = function(x) exp(-200*(x-0.5)^2) #Initial positionfVelInitial = function(x) 0*x #Initial velocity#Run simulationdx = x[2]-x[1]r = c*dt/dxn = length(x)t = seq(0,tMax,dt) #Time vectorm =length(t) + 1 |
Now iteratively compute u(x,t) by imposing the following boundary conditions
1. u(0,t) = 0
2. u(L,t) = (1/10).sin(t/10)
along with the following initial conditions
1. u(x,0) = exp(-500.(x-1/2)2)
2. ∂u(x,0)/∂t = 0.x
as defined in the above code snippet.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
#Create tri-diagonal matrix A here, as described in the algorithm#Impose initial conditionu = matrix(rep(0, n*m), nrow=m)u[1,] = fPosInitial(x)u[1,1] = fLeft(0)u[1,n] = fRight(0)for (i in 1:length(t)) { #Find solution at next time step if (i == 1) { u[2,] = 1/2*(A%*%u[1,]) + dt*fVelInitial(x) } else { u[i+1,] = (A%*%u[i,])-u[i-1,] } u[i+1,1] = fLeft(t[i]) #Impose left B.C. u[i+1,n] = fRight(t[i]) #Impose right B.C.} |
The following animation shows the output of the above implementation of the solution of wave PDE using R, it shows how the waves propagate, given a set of BCs and ICs.
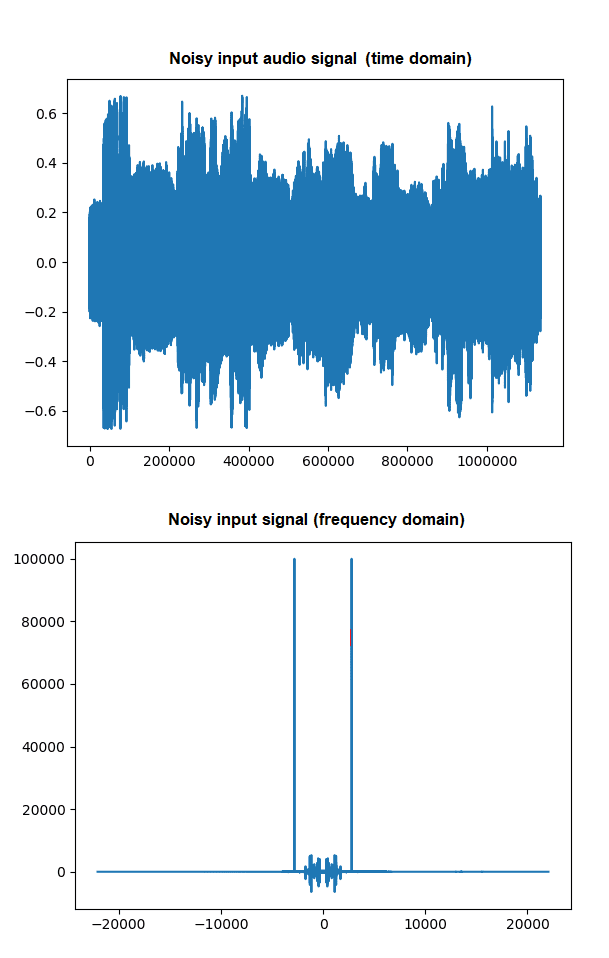
Some audio processing: De-noising an audio file with Fourier Transform
Let’s denoise an input noisy audio file (part of the theme music from Satyajit Ray’s famous movie পথের পাঁচালী, Songs of the road) using python scipy.fftpack module’s fft() implementation.
The noisy input file was generated and uploaded here.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
from scipy.io import wavfileimport scipy.fftpack as fpimport numpy as npimport matplotlib.pylab as plt# first fft to see the pattern then we can edit to see signal and inverse# back to a better soundFs, y = wavfile.read('pather_panchali_noisy.wav') # can be found here: "https://github.com/sandipan/edx/blob/courses/pather_panchali_noisy.wav" data-mce-href="https://github.com/sandipan/edx/blob/courses/pather_panchali_noisy.wav".# you may want to scale y, in this case, y was already scaled in between [-1,1]Y = fp.fftshift(fp.fft(y)) #Take the Fourier series and take a symmetric shiftfshift = np.arange(-n//2, n//2)*(Fs/n)plt.plot(fshift, Y.real) #plot(t, y); #plot the sound signalplt.show() |
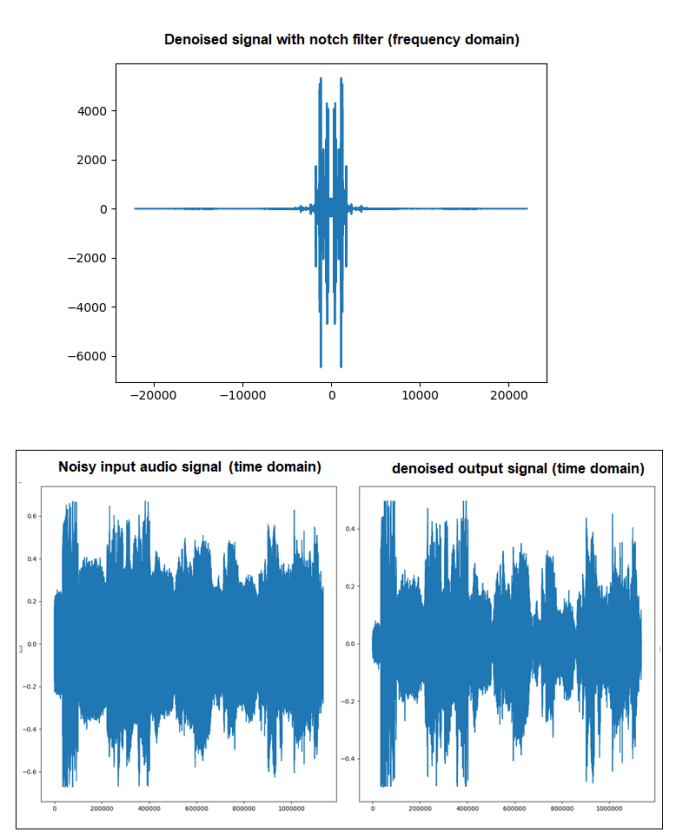
You will obtain a figure like the following:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
L = len(fshift) #Find the length of frequency valuesYfilt = Y# find the frequencies corresponding to the noise hereprint(np.argsort(Y.real)[::-1][:2])# 495296 639296Yfilt[495296] = Yfilt[639296] = 0 # find the frequencies corresponding to the spikesplt.plot(fshift, Yfilt.real)plt.show()soundFiltered = fp.ifft(fp.ifftshift(Yfilt)).realwavfile.write('pather_panchali_denoised.wav', Fs, soundNoisy) |