The explanation of Logistic Regression as a Generalized Linear Model and use as a classifier is often confusing.
In this article, I try to explain this idea from first principles. This blog is part of my forthcoming book on the Mathematical foundations of Data Science. If you are interested in knowing more, please follow me on linkedin Ajit Jaokar
We take the following approach:
- We see first briefly how linear regression works
- We then explore the assumptions and limitations of linear regression.
- Following this, we then show how these limitations can be overcome by the Generalized Linear Model (GLM)
- Finally, we explore Logistic Regression as a GLM
Explanation of Linear Regression
Machine learning involves creating a model of a process. To create a model of a process, we need to identify patterns in data. Broadly, patterns in data can be of two types: The signal (data generating process) and the variation (error generation process). The simplest model to start off with is the Linear Regression model. Linear models have some advantages – for example, they are relatively simple to implement, and many phenomenon can be modelled using linear regression
Assumptions of Linear Regression
Linear regression has the following requirements (assumptions for use)
- As per the name, Linear regression needs the relationship between the independent and dependent variables to be linear.
- the linear regression analysis requires all variables to be multivariate normal distribution.
- No multicollinearity in the data. Multicollinearity occurs when the independent variables are highly correlated with each other.
- linear regression analysis requires that there is little or no autocorrelation in the data. Autocorrelation is the correlation of a signal with a delayed copy of itself as a function of delay.
- Homoscedasticity (the residuals are equal across the regression line).
Overcoming the requirement that the dependent(response) variable is of normal distribution
The requirement that the response variable is of normal distribution excludes many cases such as:
- Where the response variable is expected to be always positive and varying over a wide range or
- Where constant input changes lead to geometrically varying, rather than continually varying, output changes.
We can illustrate these using examples: Suppose we have a model which predicts that a 10 degree temperature decrease would lead to 1,000 fewer people visiting the beach. This model does not work over small and large beaches. (Here, we could consider a small beach as one where expected attendance is 50 people and a large beach as one where the expected attendance was 10,000.). For the small beach (50 people), the model implies that -950 people would attend the beach. This prediction is obviously not correct. This model would also not work if we had a situation where we had an output that was bounded on both sides – for example in the case of a yes/no choice. This is represented by a Bernoulli variable where the probabilities are bounded on both ends (they must be between 0 and 1). If our model predicted that a change in 10 degrees makes a person twice as likely to go to the beach, as temperatures increases by 10 degrees, this model does not work because probabilities cannot be doubled.
Generalised linear models (GLM) cater to these situations by allowing for response variables that have arbitrary distributions (other than only normal distributions), and by using an arbitrary function of the response variable (called the link function) to vary linearly with the predicted values (rather than assuming that the response itself must vary linearly with the predictor). Thus, in a generalised linear model (GLM), each outcome Y of the dependent variables is assumed to be generated from the exponential family of distributions (which includes distributions such as the normal, binomial, Poisson and gamma distributions, among others). GLM thus expands the scenarios in which linear regression can apply by expanding the possibilities of the outcome variable. GLM uses the maximum likelihood estimation of the model parameters for the exponential family and least squares for normal linear models. (Note the section is adapted from Wikipedia)
Logistic Regression as GLM
To understand how logistic regression can be seen as GLM, we can elaborate this approach as follows:
Logistic regression measures the relationship between the dependent variable and one or more independent variables(features) by estimating probabilities using the underlying logit function. In statistics, the logit function or the log-odds is the logarithm of the odds. Given a probability p, the corresponding odds are calculated as p / (1 – p). For The logit function is the logarithm of the odds: logit(x) = log(x / (1 – x)). The Odds describes the ratio of success to ratio of failure. The Odds ratio is the ratio of odds and is calculated as the ratio of odds for each group.
The inverse of the logit function is the sigmoid function. The formula for the sigmoid function is σ(x) = 1/(1 + exp(-x)). The sigmoid function maps probabilities to the range [0, 1] – and this makes logistic regression as a classifier. Thus, many models have data generating processes that can be linearized by considering the inverse
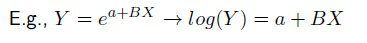
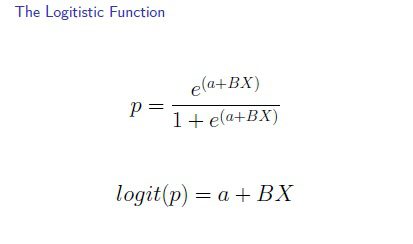
The logit and the sigmoid functions are useful in analysis because their gradients are simple to calculate. Many optimization and machine learning techniques make use of gradients ( for example in neural networks). The biggest drawback of the sigmoid function for many analytics practitioners is the so-called “vanishing gradient” problem.
This blog is part of my forthcoming book on the Mathematical foundations of Data Science. If you are interested in knowing more, please follow me on linkedin Ajit Jaokar
References
logit of logistic regression understanding the fundamentals
nathanbrixius -logit-and-sigmoid
quora.com – Why is logistic regression called regression if it does…
