Edward Teller, the famous Hungarian-American physicist, once quoted:
“A fact is a simple statement that everyone believes. It is innocent, unless found guilty. A hypothesis is a novel suggestion that no one wants to believe. It is guilty, until found effective.”
Application of hypothesis testing is predominant in Data Science. It is imperative to simplify and deconstruct it. Like a crime-fiction story, hypothesis testing, based on data, leads us from a novel suggestion to an effective proposition.
Concept
Hypothesis originates from the Greek work hupo (under) and thesis(placing). It means an idea made from limited evidence. It is a starting point for further investigation.
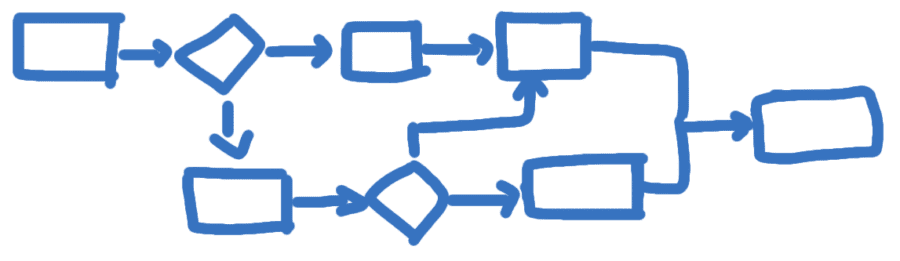
The notion is simple yet powerful. We perform hypothesis testing intuitively every day. It is a 7-step process:
- Make Assumptions.
- Take an initial position.
- Determine the alternate position.
- Set acceptance criteria
- Conduct fact based tests.
- Evaluate results. Does the evaluation support the initial position? Are we confident that the result is not due to chance?
- Reach one of the following conclusion: Reject the original position in favor of alternate position or fail to reject the initial position.
Process
Let me illustrate a story to explain the concept of hypothesis Testing. Holmavik is a small town in the western part of Iceland. This little town has its uniqueness. It is known for the Museum of Witchcraft.
Even now, there are people in Westfjords who claim to be wizards. Isildur and Gandalf are such people. Isildur and Gandalf claim to be wizards. They claim to be Clairvoyant. A statistician wants to prove or disprove this claim. They play the Clairvoyant card game.
The rules of the game are as follows:
- Isildur and Gandalf are shown the reverse of a randomly selected ten cards from a set of playing cards and asked which of the four suits it.
- They have to identify the suit the card belongs.
- This test is repeated ten times for each of them.
It is also determined that for a normal person, the average number of times the prediction is correct is around 6. This is the basis on which we will perform the hypothesis testing. We will statistically determine if they are wizards or not.
Step 1: Make Assumptions
Different kinds of hypothesis testing make different assumptions. Assumptions are related to the distribution of data, sampling, and linearity. Some of the common assumptions made are:
- Distribution: Data follows a particular distribution. Understand the underlying pattern of data. The distribution of a lot of naturally occurring data points like stock market data, human weights, and heights, salaries of people drinking in a bar, etc., can be approximated by the normal distribution. Normal distribution simply means that a lot of observations are in the middle. Fewer observations are greater or lesser than the middle value. The middle value is also called as the median.
- Sampling: It is assumed that the data that is sampled for the test are randomly selected. No bias.
For the clairvoyant card game, the following assumptions are correct:
- In the clairvoyant card game, the distribution of card selected will be normally distributed. This is true as the cards are randomly selected. Random selection of card means that each of the ten cards that will be picked has an equal probability of being selected for the test.
- The cards in question are not biased.
Step 2: The NULL Hypothesis (Ho)
The null hypothesis is the initial position. It is the status-quo position. It is the position that is rejected or fails to be rejected. It is the position that needs to be validated. It is the position that needs to be tested.
For the clairvoyant card game, the NULL hypothesis the following:
- H0: Isildur/Gandalf is not a clairvoyant.
He is simply guessing. He is lucky.
Step 3: The Alternate Hypothesis (Ha)
The alternate hypothesis is the contrary position to NULL hypothesis. If there are statistically significant evidences that suggest that the alternate hypothesis is valid, then the NULL hypothesis is rejected.
For the clairvoyant card game, the alternate hypothesis is the following:
- Ha: Isildur/Gandalf is a clairvoyant.
Step 4: Set Acceptance Criteria
The NULL and alternate hypothesis is defined. The status-quo is the NULL hypothesis. Now, a threshold needs to be set. We know that an average individual i.e. someone who is not a wizard would get it correct six times out of 10. If Isildur and Gandalf can predict the more than six correct cards in a test, then there is more evidence that they may indeed be wizards. A metric called as t-statistics calculates how far the estimated value is from the hypothesized value. High t-statistics makes the alternate hypothesis look more and more plausible.
The hypothesis test results may go wrong. There are four possible scenarios:
- Test finds that Isildur/Gandalf is a clairvoyant. He is a clairvoyant.
- Test finds that Isildur/Gandalf is a not clairvoyant. He is not a clairvoyant.
- Test finds that Isildur/Gandalf is a clairvoyant. He is not a clairvoyant.
- Test finds that Isildur/Gandalf is a not clairvoyant. He is a clairvoyant.
The test hits the bullseye for outcomes 1 and two is correct. The test fizzles out for outcomes 3 and 4.
- Outcome 3 rejects the NULL hypothesis when it is true. This is a false positive. This error is also called as Type I error.
- Outcome 3 accepts the NULL hypothesis when it is false. This is a false negative. This error is also called as Type II error.
Like all statistical testing, hypothesis testing has to deal with uncertainty. It has to deal in probabilities. There are no absolutes.
A probability level needs to be set such that the chance of Type I error occurring is established. This level is called as the significance level. The alpha (α) denotes it. A lower α means that the test is very stringent. A relatively higher α means that the test is not so strict. The value of α is set based on the nature of the hypothesis test. Typical values are 0.001, 0.05 or 0.1
What if the value observed is by mere chance? What if it is just a coincidence? What if they are just lucky on the very day when the test was conducted? This uncertainty needs to be mitigated. Hypothesis testing has a metric that takes care of this uncertainty. p-value is that metric.
The p-value is expressed as a probability. It means that its value is between 0 and 1. The p-value is the probability that the t-statistic observed by chance under the assumption that NULL hypothesis is true.
For the clairvoyant card game, it was decided that if Isildur can guess more than 8 cards correctly then the alternative hypothesis is plausible. He may be indeed a clairvoyant. The t-statistics is 8.
Being a clairvoyant is no life threatening. No one is in danger. The significance level was set at 0.05. The α is 0.05.
Step 5: Conduct Tests
The action happens. The statisticians test the clairvoyance of Isildur and Gandalf. The cards are shown. The Predictions are made. The outcomes are noted. The process is repeated ten times. A Statistical engine runs on the collected data. The result is the following:
Isildur:
- t-statistics: 8
- p-value: 0.1
-Gandalf:
- t-statistics: 9
- p-value: 0.01
Step 6: Evaluate Result
A comparison between the probability (p-value) and the significance levels yields the following result:
For Isildur:
- The t-statistics is 8. It means, on an average, he has predicted eight cards correctly. It is higher than what a normal human can predict.
- The p-value is 0.1. It implies that probability that the observed t-statistics is due to chance is 10%. The p-value is high.
- The set significance level (α) is 0.05. It translates to 5%.
- p-value is greater than the set significance level i.e. 10% > 5%.
For Gandalf:
- The t-statistics is 9. It means, on an average, he has predicted nine cards correctly. It is higher than what a normal human can predict.
- The p-value is 0.01. It implies that probability that the observed t-statistics is due to chance is only 1%.
- The set significance level (α) is 0.05. It translates to 5%.
- p-value is lower than the set significance level i.e. 1% < 5%.
Step 7: Conclude
The tests have ended. The metrics are known. Who is the real wizard?
For Isildur: The p-value is greater than the set significance level (10% > 5%). Even though, on an average, he has predicted eight cards correctly; statistically, the conclusion is the following:
- Conclusion for Isildur: There is no substantial evidence against the NULL hypothesis. The NULL hypothesis fails to be rejected.
For Gandalf: On an average, he has predicted nine cards correctly. The p-value is lower than the set significance level (1% < 5%).
- Conclusion for Gandalf: There is sound evidence against the NULL hypothesis. The NULL hypothesis is rejected. Alternate hypothesis is accepted.
Isildur is devastated. Gandalf is elated. However, Isildur may take solace for it is not proven that he not a clairvoyant. The NULL hypothesis is failed to be rejected. It doesn’t mean that alternate hypothesis is not true. It only means that there is not enough evidence to reject the NULL hypothesis. Status-quo prevails for Isildur.
Conclusion
There is no need to perform a hypothesis test to find who is the wizard among Isildur and Gandalf. We all know that Gandalf is the wizard.
The hypothesis testing is one of the cornerstone concepts in machine learning. A lot of evaluation methods use hypothesis testing to evaluate the robustness of the models. We will deep-dive further into its constructs as we journey through this series.
