This article was written by Jim Frost.
In regression analysis, curve fitting is the process of specifying the model that provides the best fit to the specific curves in your dataset. Curved relationships between variables are not as straightforward to fit and interpret as linear relationships.
For linear relationships, as you increase the independent variable by one unit, the mean of the dependent variable always changes by a specific amount. This relationship holds true regardless of where you are in the observation space.
Unfortunately, the real world isn’t always nice and neat like this. Sometimes your data have curved relationships between variables. In a curved relationship, the change in the dependent variable associated with a one unit shift in the independent variable varies based on the location in the observation space. In other words, the effect of the independent variable is not a constant value.
Read my post where I discuss how to interpret regression coefficients for both linear and curvilinear relationships to see this in action.
In this post, I cover various curve fitting methods using both linear regression and nonlinear regression. I’ll also show you how to determine which model provides the best fit.
Why You Need to Fit Curves in a Regression Model:
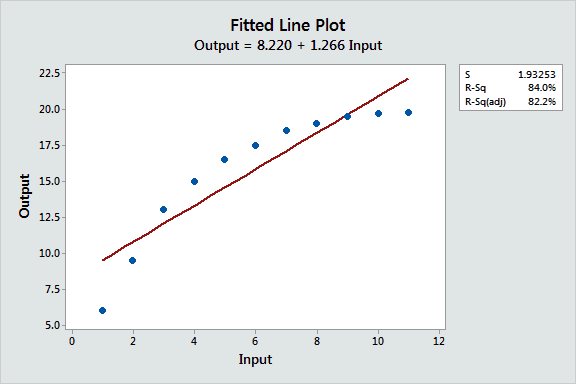
The fitted line plot below illustrates the problem of using a linear relationship to fit a curved relationship. The R-squared is high, but the model is clearly inadequate. You need to do curve fitting!
When you have one independent variable, it’s easy to see the curvature using a fitted line plot. However, with multiple regression, curved relationships are not always so apparent. For these cases, residual plots are a key indicator for whether your model adequately captures curved relationships.
If you see a pattern in the residual plots, your model doesn’t provide an adequate fit for the data. A common reason is that your model incorrectly models the curvature. Plotting the residuals by each of your independent variables can help you locate the curved relationship.
In others cases, you might need to depend on subject-area knowledge to do curve fitting. Previous experience or research can tell you that the effect of one variable on another varies based on the value of the independent variable. Perhaps there’s a limit, threshold, or point of diminishing returns where the relationship changes?
To compare curve fitting methods, I’ll fit models to the curve in the fitted line plot above because it is not an easy fit. Let’s assume that these data are from a physical process with very precise measurements. We need to produce accurate predictions of the output for any specified input.
Curve Fitting using Polynomial Terms in Linear Regression:
Despite its name, you can fit curves using linear regression. The most common method is to include polynomial terms in the linear model. Polynomial terms are independent variables that you raise to a power, such as squared or cubed terms.
To determine the correct polynomial term to include, simply count the number of bends in the line. Take the number of bends in your curve and add one for the model order that you need. For example, quadratic terms model one bend while cubic terms model two. In practice, cubic terms are very rare, and I’ve never seen quartic terms or higher. When you use polynomial terms, consider standardizing your continuous independent variables.
To read the full original article and learn more about curve fitting with nonlinear regression and the curve fitting effectiveness of different models, click here. For more curve fitting related articles on DSC click here.
DSC Resources
- Services: Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Contributors: Post a Blog | Ask a Question
- Follow us: @DataScienceCtrl | @AnalyticBridge
Popular Articles