Introduction

Co-relation does not equal causation – is a mantra drilled into a Data Scientist from an early age

That’s fine ..

But very few talk of the follow-on question ..

How exactly do you determine causation?

This problem is further compounded because most books and examples are based on standard datasets (ex: Boston, Iris etc) .

These examples do not discuss causation because the features chosen are already determined to be causal (ex the factors affecting house prices are chosen to be causal)

So, if we start from the beginning (without simplified examples) how do you know if a particular variable is a causal variable?

Firstly, causality cannot be determined from data alone.

Data gives co-relation, but data alone cannot determine causation

To determine causation, we need to perform an experiment or a controlled study

Background

In a statistical sense, two or more variables are related if their values change correspondingly i.e. increase or decrease together. On the other hand, if there is a causal relationship between two variables, then the occurrence of one depends on the other i.e. they exhibit a cause and effect relationship. For example, smoking causes lung cancer is a causal relationship while smoking is correlated to alcoholism but does not cause alcoholism.  

Correlation is typically measured using Pearson’s coefficient or Spearman’s coefficient. If there is correlation, then further investigation is needed to establish if there is a causal relationship.

How can causation be established?

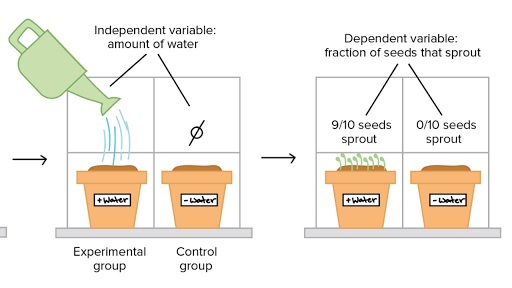
The most effective way of establishing causation is by means of a controlled study.

In a controlled study, the sample or population is split in two, with both groups being comparable in almost every way.

The two groups then receive different treatments, and the outcomes of each group are assessed. 

For example, in medical research, one group is given a placebo whereas the other group is given a new medication.

So, in a nutshell - "To find out what happens when you change something, it is necessary to change it."...There are things you learn from perturbing a system that you'll never find out from any amount of passive observation.

Source: http://people.umass.edu/~stanek/pdffiles/causal-holland.pdf

The design of controlled experiments is a non-trivial exercise:

• You may have measurement error problems
• subjects might drop the study or not follow instructions, among other issues.
• You will need to make assumptions about how things are related to determine inference.
• You may have incomplete/imprecise data
• Target causal quantity of interest may not be well defined
• Confounding variables. A confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association.
• Selection bias (self-selection, truncated samples)
• Measurement error (that can induce confounding, not only noise)
• Misspecification (e.g., wrong functional form)
• External validity problems (wrong inference to target population)

Adapted from source

Finally, there are some methods like the Granger causality that is a statistical method which demonstrates some causality (with limitations)

Sources

https://abs.gov.au/websitedbs/a3121120.nsf/home/statistical+languag...

Why do we need causality in data science

Image source: Khan academy