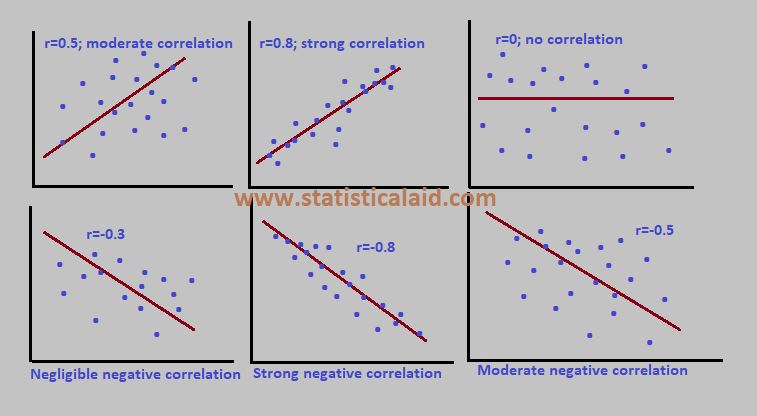
Correlation Analysis
The relationship between two or more random variables are generally defined as the correlation. It is the major part of bivariate analysis. When variables are found to be related, we often want to know how close the relationship is. The study of the relationship is known as correlation analysis. The primary objective of correlation is to measure the strength or degree of linear association between two or more variables. For example, we may be interested in measuring the relationship between the-
- Height and weight of the people of certain area.
- Ages of husband and their wives.
- Amount of rice production and fertilizer.
- Income and expenditure.
- Total sales and experience of the sales persons..etc.
Correlation vs Regression
The contradictions between regression and correlation are given below-
In correlation, we are generally interested in the measurement of the linear relationship between two or more variables. On the other hand, regression analysis doesn’t asses such relationship.
In correlation analysis we consider any two or more variables. On the otherhand, in regression there must need one dependent and one or more independent variables. Here the dependent variable is stochastic or random variable and the independent or explanatory variable is fixed.
Correlation analysis provides a means of measuring the goodness of fit of the estimated regression line to the observed statistical data. On the other hand, regression analysis doesn’t provide any means to measure the goodness of fit but it tells about the average amount of change in the dependent variable to one unit change in the independent variable.