A myriad of options exist for classification. In general, there isn’t a single “best” option for every situation. That said, three popular classification methods— Decision Trees, k-NN & Naive Bayes—can be tweaked for practically every situation.
Overview
Naive Bayes and K-NN, are both examples of supervised learning (where the data comes already labeled). Decision trees are easy to use for small amounts of classes. If you’re trying to decide between the three, your best option is to take all three for a test drive on your data, and see which produces the best results.
If you’re new to classification, a decision tree is probably your best starting point. It will give you a clear visual, and it’s ideal to get a grasp on what classification is actually doing. K-NN comes in a close second; Although the math behind it is a little daunting, you can still create a visual of the nearest neighbor process to understand the process. Finally, you’ll want to dig into Naive Bayes. The math is complex, but the result is a process that’s highly accurate and fast—especially when you’re dealing with Big Data.
Where Bayes Excels
1. Naive Bayes is a linear classifier while K-NN is not; It tends to be faster when applied to big data. In comparison, k-nn is usually slower for large amounts of data, because of the calculations required for each new step in the process. If speed is important, choose Naive Bayes over K-NN.
2. In general, Naive Bayes is highly accurate when applied to big data. Don’t discount K-NN when it comes to accuracy though; as the value of k in K-NN increases, the error rate decreases until it reaches that of the ideal Bayes (for k→∞).
3. Naive Bayes offers you two hyperparameters to tune for smoothing: alpha and beta. A hyperparameter is a prior parameter that are tuned on the training set to optimize it. In comparison, K-NN only has one option for tuning: the “k”, or number of neighbors.
4. This method is not affected by the curse of dimensionality and large feature sets, while K-NN has problems with both.
5. For tasks like robotics and computer vision, Bayes outperforms decision trees.
Where K-nn Excels
1. If having conditional independence will highly negative affect classification, you’ll want to choose K-NN over Naive Bayes. Naive Bayes can suffer from the zero probability problem; when a particular attribute’s conditional probability equals zero, Naive Bayes will completely fail to produce a valid prediction. This could be fixed using a Laplacian estimator, but K-NN could end up being the easier choice.
2. Naive Bayes will only work if the decision boundary is linear, elliptic, or parabolic. Otherwise, choose K-NN.
3. Naive Bayes requires that you known the underlying probability distributions for categories. The algorithm compares all other classifiers against this ideal. Therefore, unless you know the probabilities and pdfs, use of the ideal Bayes is unrealistic. In comparison, K-NN doesn’t require that you know anything about the underlying probability distributions.
4. K-NN doesn’t require any training—you just load the dataset and off it runs. On the other hand, Naive Bayes does require training.
5. K-NN (and Naive Bayes) outperform decision trees when it comes to rare occurrences. For example, if you’re classifying types of cancer in the general population, many cancers are quite rare. A decision tree will almost certainty prune those important classes out of your model. If you have any rare occurrences, avoid using decision trees.
Where Decision Trees Excel
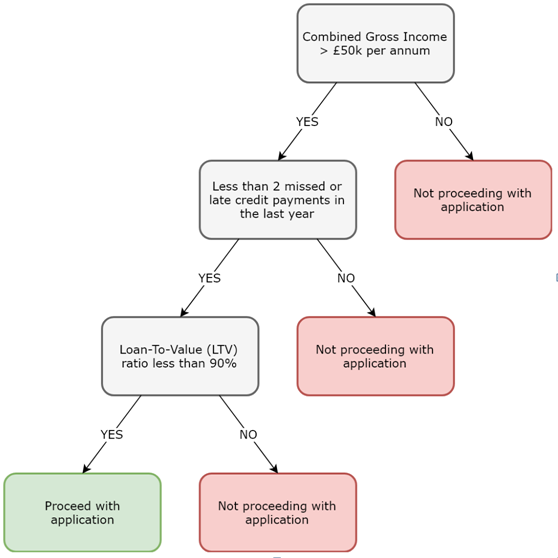 Image: Decision tree for a mortgage lender.
Image: Decision tree for a mortgage lender.
1. Of the three methods, decision trees are the easiest to explain and understand. Most people understand hierarchical trees, and the availability of a clear diagram can help you to communicate your results. Conversely, the underlying mathematics behind Bayes Theorem can be very challenging to understand for the layperson. K-NN meets somewhere in the middle; Theoretically, you could reduce the K-NN process to an intuitive graphic, even if the underlying mechanism is probably beyond a layperson’s level of understanding.
2. Decision trees have easy to use features to identify the most significant dimensions, handle missing values, and deal with outliers.
3. Although over-fitting is a major problem with decision trees, the issue could (at least, in theory) be avoided by using boosted trees or random forests. In many situations, boosting or random forests can result in trees outperforming either Bayes or K-NN. The downside to those add-ons are that they add a layer of complexity to the task and detract from the major advantage of the method, which is its simplicity.
More branches on a tree lead to more of a chance of over-fitting. Therefore, decision trees work best for a small number of classes. For example, the above image only results in two classes: proceed, or do not proceed.
4. Unlike Bayes and K-NN, decision trees can work directly from a table of data, without any prior design work.
5. If you don’t know your classifiers, a decision tree will choose those classifiers for you from a data table. Naive Bayes requires you to know your classifiers in advance.
References
Decision tree vs. Naive Bayes classifier
Comparison of Naive Basian and K-NN Classifier
Doing Data Science: Straight Talk from the Frontline
