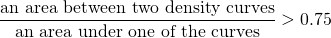There are many ways to choose features with given data, and it is always a challenge to pick up the ones with which a particular algorithm will work better. Here I will consider data from monitoring performance of physical exercises with wearable accelerometers, for example, wrist bands.
In this project, researchers used data from accelerometers on the belt, forearm, arm, and dumbbell of few participants. They were asked to perform barbell lifts correctly, marked as “A”, and incorrectly with four typical mistakes, marked as “B”, “C”, “D” and “E”. The goal of the project is to predict the manner in which they did the exercise.
There are 52 numeric variables and one classification variable, the outcome. We can plot density graphs for first 6 features, which are in effect smoothed out histograms.
We can see that data behaviors are complicated. Some of features are bimodal and even multimodal. These properties could be caused by participants’ different sizes or training levels or something else, but we do not have enough information to check it out. Nevertheless it is clear that our variables do not obey normal distribution. Therefore we are better with algorithms which do not assume normality, like trees and random forests. We can visualize the algorithms work in the following way: as finding vertical lines which divide areas under curves such that areas to the right and to to left of the line are significantly different for different outcomes.
There are a number of ways to distinguish functions analytically on an interval in Functional Analysis. It looks like the most suitable is to consider areas between curves. Clearly, we should scale it with respect to the size of the curves. For every feature I will consider all pairs of density curves to find out if they are sufficiently different. Here is my final criterion:
If there is a pair for a feature which satisfies it then the feature is chosen for a prediction. As result I got 21 features for a random forests algorithm. The last one yielded accuracy 99% for the model itself and on a validation set. I checked how many variables we need for the same accuracy with PCA preprocessing, and it was 36. Mind you that the variables will be scaled and rotated, and that we still use the same original 52 features to construct them. Thus more efforts are needed to construct a prediction and to explain it. While with the above method it is easier, since areas under curves represent numbers of observations.
