Home » Uncategorized

Automated Machine Learning Hyperparameter Tuning in Python

This article was written by William Koehrsen

A complete walk through using Bayesian optimization for automated hyperparameter tuning in Python

Tuning machine learning hyperparameters is a tedious yet crucial task, as the performance of an algorithm can be highly dependent on the choice of hyperparameters. Manual tuning takes time away from important steps of the machine learning pipeline like feature engineering and interpreting results. Grid and random search are hands-off, but require long run times because they waste time evaluating unpromising areas of the search space. Increasingly, hyperparameter tuning is done by automated methods that aim to find optimal hyperparameters in less time using an informed search with no manual effort necessary beyond the initial set-up.

Bayesian optimization, a model-based method for finding the minimum of a function, has recently been applied to machine learning hyper parameter tuning, with results suggesting this approach can achieve better performance on the test set while requiring fewer iterations than random search. Moreover, there are now a number of Python libraries that make implementing Bayesian hyperparameter tuning simple for any machine learning model.

In this article, we will walk through a complete example of Bayesian hyperparameter tuning of a gradient boosting machine using the Hyperopt Library. In an an earlier article I outlined the concepts behind this method, so here we will stick to the implementation. Like with most machine learning topics, it’s not necessary to understand all the details, but knowing the basic idea can help you use the technique more effectively!

All the code for this article is available as a Jupyter Notebook on Github.

2808362756

Table of Contents

  • Bayesian Optimization Methods 
  • Four Parts of Optimization Problem
  • Objective Function
  • Domain Space
  • Optimization Algorithm 
  • Result History
  • Optimization
  • Results
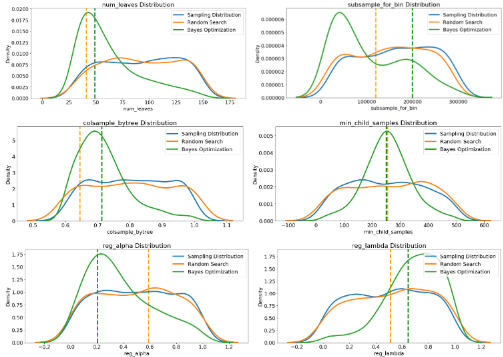
  • Visualization Search Results
  • Evolution of Search
  • Continue Searching
  • Conclusions

Bayesian Optimization Methods

As a brief primer, Bayesian Optimization finds the value that minimizes an objective function by building a surrogate function (probability model) based on past evaluation results of the objective. The surrogate is cheaper to optimize than the objective, so the next input values to evaluate are selected by applying a criterion to the surrogate (often Expected Improvement). Bayesian methods differ from random or grid search in that they use past evaluation results to choose the next values to evaluate.The concept is limit expensive evaluations of the objective function by choosing the next input values based on those that have done well in the past.

In the case of hyperparameter optimization, the objective function is the validation error of a machine learning model using a set of hyperparameters. The aim is to find the hyperparameters that yield the lowest error on the validation set in the hope that these results generalize to the testing set. Evaluating the objective function is expensive because it requires training the machine learning model with a specific set of hyperparameters. Ideally, we want a method that can explore the search space while also limiting evaluations of poor hyperparameter choices. Bayesian hyper parameter tuning uses a continually updated probability model to “concentrate” on promising hyperparameters by reasoning from past results.

To read the rest of the article, click here. To find more articles involving Bayesian Optimization, click here. 

DSC Resources

Tags:

Related Content