Guest blog post by Brian Rowe
Another big part of the food supply comes from ranches and farms that raise and slaughter various livestock. While ranching is sometimes bundled with agriculture, I discussed farming in Big Data in Agriculture, so we’ll focus on ranching this time around. Somewhat surprising is that big data usage in ranching appears more limited than in farming. That said, there are a number of novel uses of technology and data in animal husbandry.
Land Use Optimization
At a high level, the goals of ranching and farming are the same as any business: increase yields and lower costs. Production maximization has long played a role in large operations. A twist to the optimization problem is land use optimization and how that can affect yields. According to NASA, “Australia’s rangelands provide an opportunity to sustainably produce meat without contributing to deforestation” if properly managed. This sort of optimization is made possible by big data coming from satellites. The same article cites how some West African nations use satellite data “to identify areas with agricultural potential and to estimate the amount of food available.” Growing up in rural Colorado, the most advanced tech I saw at ranches were solar powered fences and artificial insemination. Clearly a lot has changed. From a supply chain perspective, these trends also demonstrate how just-in-time manufacturing can be extended to resource allocation.
From a technical perspective, crop and livestock rotation will become outputs of a multi-objective optimization problem. I imagine that the challenge will be less about the optimization and more about the inelasticity of “bioprocesses”. Aside from slaughter or transfer to somewhere else, there aren’t too many options for reducing “inventory”. Presumably these issues already exist, so any solution is bound to be an improvement. Ultimately, there is a race to avoid the outcome that the U.N. foresees: the majority of humans eating insects as a primary source of protein. Even if that future is unavoidable (not necessarily bad), presumably similar techniques can be used to maximize insect yields.
Sensors and IoT
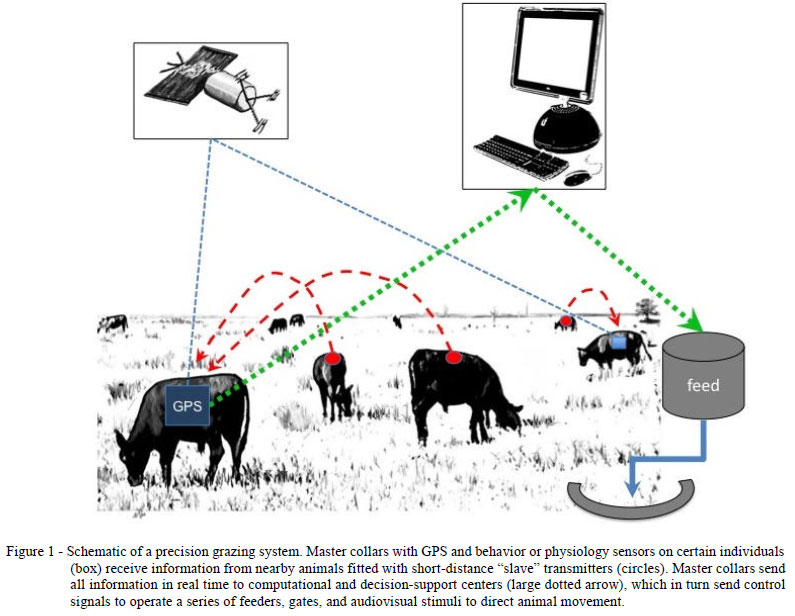
Technology advancements are driving parralel trends in agriculture and ranching. While satellite imagery offers a big picture overview, sensors provide a micro view of individual plants and animals. RFID tags are a first step enabling real-time tracing of an animal. Equally important is the assignment of a unique identifier to facilitate storing electronic records that can be merged into a centralized dataset. RFID is fundamentally passive, whereas sensors are active. This is where biosensors and Precision Livestock Farming (PLF) come into play. PLF is a comprehensive approach to livestock management and animal welfare. The goal is “continuous, fully automatic monitoring and improvement of animal health and welfare, product yields and environmental impacts” Some of the sensors developed to achieve this are surprisingly simple and surprisingly clever, such as sensors that monitor the vocalizations of livestock to determine stress, illness, etc. These advances can also “raise milk yields, while also increasing cows’ life expectancy and reducing their methane emissions by up to 30%” (CEMA). The Biosensors in Agriculture workshop held in the UK presents even more exciting examples.
Other notable research around PLF include image analysis to monitor animal welfare and
classifying the behavior of cattle and fowl based on GPS movements. According to one paper, a decision tree was used to classify four behaviors: ruminating, foraging, standing, and walking. The features were based on distances and turning angles from the GPS data. Not surprisingly, the confusion matrix was pretty poor in terms of distinguishing between ruminating, foraging, and standing. So there’s lots of opportunities to whip out R and randomForest or party to conduct your own analysis (assuming you have access to the data).
Data and Accessibility
Big data is often synonomous with cloud computing and for ranching it’s no different. As with agriculture there are trends to centralize data to “help ranch managers track livestock, view production statistics, plan grazing rotations and generate reports that can offer insight into the health of a livestock operation.” Unlike in agriculture, it doesn’t appear that the machinery manufacturers are taking a role, although it wouldn’t surprise me if some PLF suppliers have cloud platforms for their customers. GrowSafe Systems is creating their own cloud-based dataset based on their customer data. Their system collects and forecasts “complex animal traits such as efficiency, growth, health, stress and adaptation.”
Europe has taken a different approach focusing on defining a comprehensive classification scheme for agricultural systems. Clearly the goal is data interoperability, so data can be widely shared and applied across farms and ranches. This goal is reflected in the three-level system that encompasses environmental factors and GIS data to site-specific measurements of individual animals that affect yields and animal welfare. Landcover data appears to be the most extensive, while biosensing is likely where the most immediate opportunities are to be found.
As data becomes more focused on individual sites and animals, scarcity is the word that comes to mind. In the USA public datasets don’t come anywhere near the level of detail to make a useful analysis. See data.gov for an example of a disappointing dataset. Of course it isn’t clear whether transparency of this sort is even possible. One rancher believes they have a right to privacy and shouldn’t be compelled to open their books to external scrutiny. This is understandable, but does this belief extend to data? Data privacy is a thorny issue, particularly balancing privacy, ownership, and the need for transparency vis a vis food security/safety. Eventually I think economics will force a change of heart if yields and margins increase significantly with the help of open data. However, this may take the shape of data cartels as opposed to truly open data. As big data and centralized data stores become more wide spread, this debate over data ownership will continue to be visited.
Know of some public datasets available for ranching and animal husbandry? Post links in the comments!
This post first appeared on cartesianfaith.com. Brian Lee Yung Rowe is Founder and Chief Pez Head of Pez.AI // Zato Novo, a conversational AI platform for guided data analysis and Q&A. Learn more at Pez.AI.
Follow us @IoTCtrl | Join our Community