When ever we visit a client and present our proposal, we start wondering if it will be accepted or rejected by the customer. Usually, our customer will analyze our proposal, compare it with other competitors’ and make a decision.
In order to build our commercial forecast system, we need to assign a probability to every proposal we have presented and assign a numerical value to every one of them.
One way of doing this is multiplying the value of the proposal by the probability of wining it.
Expected_income=proposal_value* proposal_probability
But, how to assign a probability to the different opportunities?
Most commercial departments calculate the probability of wining the opportunity using the knowledge, experience and instinct of the team.
And, is there any other way to calculate the chances for this opportunity to be successful?
The answer is yes. Using logistic regression, one of the most popular techniques in machine learning, it is possible to train one algorithm that calculates the probability for one commercial opportunity to be successful.
Logistic regression can be applied to many variables, but to keep it simple we will use only one, and that is the time (in days) that the opportunity has been “alive” since it was created.
The reason why we choose this variable is because most of purchasing departments need a certain time to analyze proposals and make a decision for a specific kind of product, after this time the opportunity doesn’t have many chances to be successful.
To train the model it is necessary to use the historical information and prepare the data in such a way that in the X column we have the time one opportunity was “alive” and in the Y column we place “0” or “1” depending if this opportunity was successful or not.
Using R we can perform this regression in very easily
fit <- glm(result ~ time, data = Products, family = ‘binomial’)
R will store the values for the independent variable and the intercept, so we will be able to construcnt the expression z=a*time+intercept .
Finally we calculate the time dependent probability as p(t)=sigmoid(z)
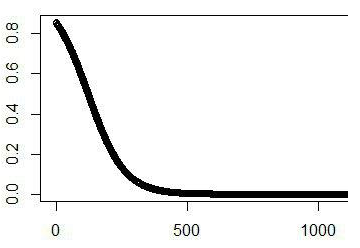 We shoul obtain a trend like this. The final shape of the curve will depend on the market nature.
We shoul obtain a trend like this. The final shape of the curve will depend on the market nature.
