This article was written by Sahil Singla.
Introduction:
In the max-pooling layer (used in almost all state of the art vision tasks and even some NLP tasks) you throw away roughly 75% of the activations. I wanted to design a new kind of pooling layer that gets rid of some of the problems associated with it.
The problems are:
- Loss of spatial information. When you throw away 75% of activations, the information about where those activations came from is lost.
- Max-pooling cannot use information from multiple activations.
- Backpropagation only improves the maxpooled activation, even though the other activations might have wrong values.
I wanted to design a new kind of pooling layer that solves as many of these problems as I could. In that process, I came up with a very simple trick to solve #2 and #3.
Idea and Motivation:
Instead of taking the max of the 4 activations, sort the 4 activations in increasing order. Multiply them by 4 weights [w1,w2,w3,w4] and add the 4 values.
Motivation behind the idea was very simple:
- This way the network remains capable of learning the good old max pooling which corresponds to [w1,w2,w3,w4] = [1,0,0,0].
- The later layers have access to more information. So in case the non-max activations are useful for decreasing the loss function, the network can just learn to use the other values.
- Gradient flows through all 4 values in the previous layer (compared to only 1 in max pooling).
So my hunch was, due to these reasons this idea would do much better than max pooling. And this was one of the very rare DL experiments where everything worked out exactly as I had expected.
Concrete definition:
Let the output of the layer before pooling be a tensor T, of size [B, H, W, C]. I define a hyperparameter pool_range which can be one of [1,2,3,4]. pool_range specifies how many of the activations (in sorted order are to be kept). Meaning given 4 activations of the tensor T which are to be pooled, I first sort them in the order [a1, a2, a3, a4] where a1 ≥ a2 ≥ a3 ≥ a4. Then I keep the first pool_range of them. I call this new vector activation vector.
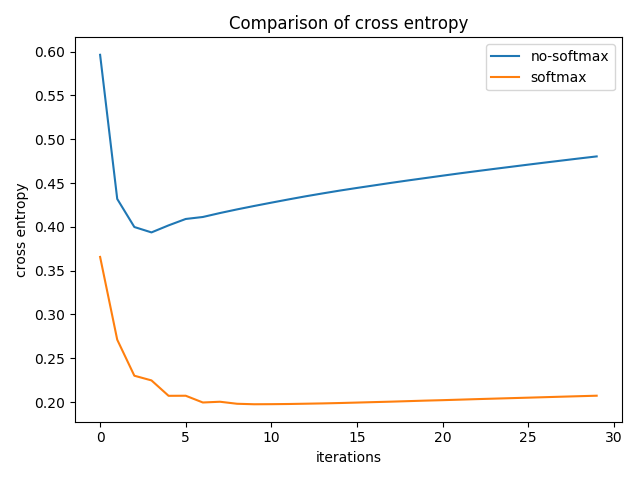
I define a weight vector of size pool_range [w{1},…. w{pool_range}]. One caveat here is that if any one of these weights is negative, then the assumption that the activation vector is sorted by strength and we are taking a weighted average will not hold true. So instead of using the weights directly I take a softmax over the weight vector and multiply the result with the activation vector. To test the importance of adding a softmax, I conducted a toy experiment on the cluttered-mnist dataset, with and without softmax and pool_range=3. Following were the results on the test dataset.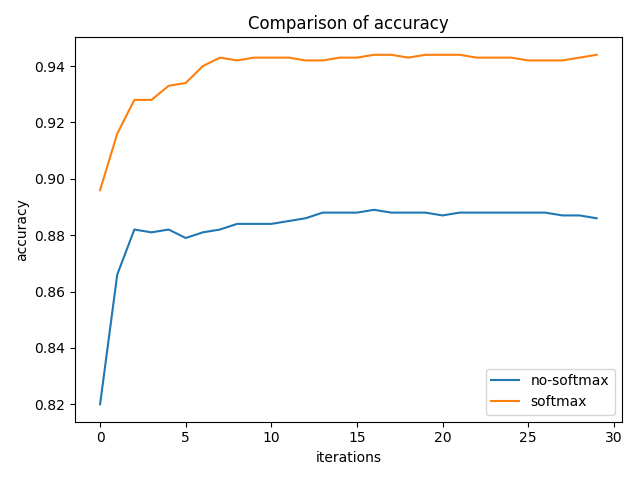
Clearly, softmax is the winner here.
I could have also used different weights for different channels but in order to keep this comparable to max_pooling, I used the same 4 weights across channels.
Implementation details:
I write the code for this layer in tensorflow. tensorflow’s top_k layer was fast on the CPU bet terribly slow on the GPU. So instead of using that, I wrote my own sorting routine for sorting the 4 floats.
Results:
I tried this idea on many different datasets and architectures and it outperformed the baseline max-pooling on all of them. All experiments were performed with all four values of pool_range: 1,2,3,4. pool_range=1 corresponds to max pooling.
To read the full original article click here. For more convergence net related articles on DSC click here.
DSC Resources
- Services: Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Contributors: Post a Blog | Ask a Question
- Follow us: @DataScienceCtrl | @AnalyticBridge
Popular Articles