In a previous blog-post we have seen how we can use Signal Processing techniques for the classification of time-series and signals.

A very short summary of that post is: We can use the Fourier Transform to  transform a signal from its time-domain to its frequency domain. The peaks in the frequency spectrum indicate the most occurring frequencies in the signal. The larger and sharper a peak is, the more prevalent a frequency is in a signal. The location (frequency-value) and height (amplitude) of the peaks in the frequency spectrum then can be used as input for Classifiers like Random Forest or Gradient Boosting.

This simple approach works surprisingly well for many classification problems. In that blog post we were able to classify the Human Activity Recognition dataset with a ~91 % accuracy.

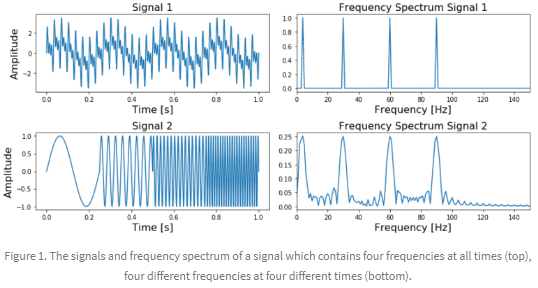
The general rule is that this approach of using the Fourier Transform will work very well when the frequency spectrum is stationary. That is, the frequencies present in the signal are not time-dependent; if a signal contains a frequency of x  this frequency should be present equally anywhere in the signal.
The more non-stationary/dynamic a signal is, the worse the results will be. That’s too bad, since most of the signals we see in real life are non-stationary in nature. Whether we are talking about ECG signals, the stock market, equipment or sensor data, etc, etc, in real life problems start to get interesting when we are dealing with dynamic systems. A much better approach for analyzing dynamic signals is to use the Wavelet Transform instead of the Fourier Transform.

Even though the Wavelet Transform is a very powerful tool for the analysis and classification of time-series and signals, it is unfortunately not known or popular within the field of Data Science. This is partly because you should have some prior knowledge (about signal processing, Fourier Transform and Mathematics) before you can understand the mathematics behind the Wavelet Transform. However, I believe it is also due to the fact that most books, articles and papers are way too theoretical and don’t provide enough practical information on how it should and can be used.
In this blog-post we will see the theory behind the Wavelet Transform (without going too much into the mathematics) and also see how it can be used in practical applications. By providing Python code at every step of the way you should be able to use the Wavelet Transform in your own applications by the end of this post.

The contents of this blogpost are as follows:

1. Introduction
2. Theory
   • 2.1 From Fourier Transform to Wavelet Transform
   • 2.2 How does the Wavelet Transform work?
   • 2.3 The different types of Wavelet families
   • 2.4 Continuous Wavelet Transform vs Discrete Wavelet Transform
   • 2.5 More on the Discrete Wavelet Transform: The DWT as a filter-bank.
3. Practical Applications
   • 3.1 Visualizing the State-Space using the Continuous Wavelet Transform
   • 3.2 Using the Continuous Wavelet Transform and a Convolutional Neural Network to classify signals
     • 3.2.1 Loading the UCI-HAR time-series dataset
     • 3.2.2 Applying the CWT on the dataset and transforming the data to the right format
     • 3.2.3 Training the Convolutional Neural Network with the CWT
   • 3.3 Deconstructing a signal using the DWT
   • 3.4 Removing (high-frequency) noise using the DWT
   • 3.5 Using the Discrete Wavelet Transform to classify signals
     • 3.5.1 The idea behind Discrete Wavelet classification
     • 3.5.2 Generating features per sub-band
     • 3.5.3 Using the features and scikit-learn classifiers to classify two datasets.
   • 3.6 Comparison of the classification accuracies between DWT, Fourier Transform and Recurrent Neural Networks
4. Finals Words

Read the rest of the blog-post here.