This article was written by Alberto Quesada.
The procedure used to carry out the learning process in a neural network is called the optimization algorithm (or optimizer). There are many different optimization algorithms. All have different characteristics and performance in terms of memory requirements, speed and precision.
Problem formulation
The learning problem is formulated in terms of the minimization of a loss index, f. This is a function which measures the performance of a neural network on a data set.
The loss index is, in general, composed of an error and a regularization terms. The error term evaluates how a neural network fits the data set. The regularization term is used to prevent overfitting, by controlling the effective complexity of the neural network.
The loss function depends on the adaptive parameters (biases and synaptic weights) in the neural network. We can conveniently group them together into a single n-dimensional weight vector w.
The problem of minimizing continuous and differentiable functions of many variables has been widely studied. Many of the conventional approaches to this problem are directly applicable to that of training neural networks.
One-dimensional optimization
Although the loss function depends on many parameters, one-dimensional optimization methods are of great importance here. Indeed, they are very often used in the training process of a neural network.
Certainly, many training algorithms first compute a training direction d and then a training rate η; that minimizes the loss in that direction, f(η).
In this regard, one-dimensional optimization methods search for the minimum of a given one-dimensional function. Some of the algorithms which are widely used are the golden section method and Brent’s method. Both reduce the bracket of a minimum until the distance between the two outer points in the bracket is less than a defined tolerance.
Multidimensional optimization
The learning problem for neural networks is formulated as searching of a parameter vector w∗ at which the loss function f takes a minimum value. The necessary condition states that if the neural network is at a minimum of the loss function, then the gradient is the zero vector.
The loss function is, in general, a non-linear function of the parameters. As a consequence, it is not possible to find closed training algorithms for the minima. Instead, we consider a search through the parameter space consisting of a succession of steps. At each step, the loss will decrease by adjusting the neural network parameters.
In this way, to train a neural network we start with some parameter vector (often chosen at random). Then, we generate a sequence of parameters, so that the loss function is reduced at each iteration of the algorithm. The change of loss between two steps is called the loss decrement. The training algorithm stops when a specified condition, or stopping criterion, is satisfied.
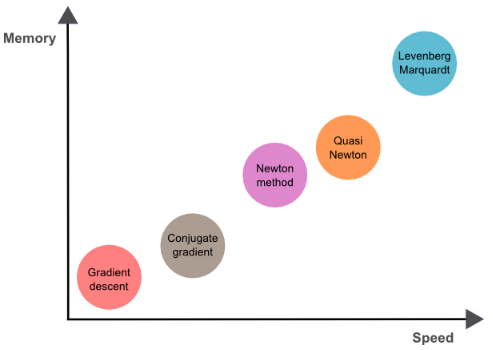
These are the main training algorithms for neural networks:
- Gradient descent
- Newton method
- Conjugate gradient
- Quasi-Newton method
- Levenberg-Marquardt algorithm
To read the whole article, with formulas and illustrations, click here.
