I’ve written several times about how the “economies of learning” are more powerful than the “economies of scale”. Through a continuous learning and refinement process, organizations can simultaneously drive down marginal costs while accelerating time-to-value and de-risking projects via digital asset re-use and refinement (see Figure 1).
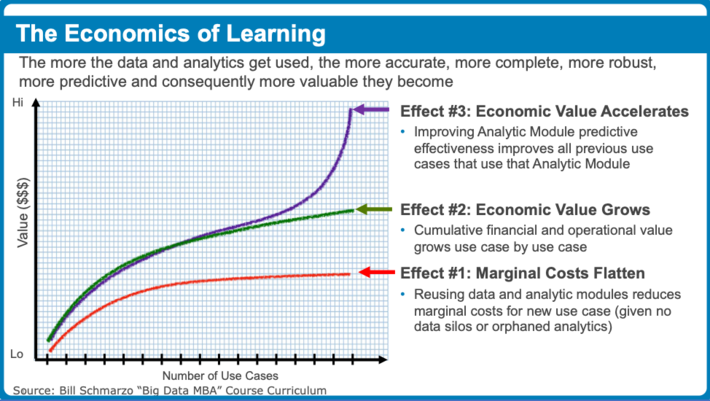
Figure 1: Exploiting the Digital Economies of Learning
Think about how us lowly humans learn. Whether trying to hit a golf ball or playing the piano or water skiing, we learn though the “feedback loop of failure”. And the more real-time, immediate that feedback loop, the more quickly we can assess what we did wrong, adjust and then try again. And while that is “feedback loop of failure” is certainly critical to human learning, guess what, it is also critical to how machines learn!
I had the fortunate opportunity (living near Stanford does have its benefits) to attend a Saturday workshop titled “Crash Course on AI” taught by Professor Ronjon Nag. The course and the associated readings helped me to better understand how machines use neural network to learn. Here is a summary of my learnings from that class (note: see the end of the blog for some very useful links on neural networks).
How Machines Learn
Meta-learning is the hot buzz word in the world of Machine Learning and Artificial Intelligence. The goal of Meta-learning is for machines to “learn how to learn” by designing algorithmic models that can learn new skills or adapt to new environments rapidly without requiring massive test data sets (Deep Learning). There are three common approaches: 1) learn an efficient distance metric (metric-based); 2) use a (recurrent) neural network with external or internal memory (model-based); 3) optimize the model parameters explicitly for fast learning (optimization-based)[1].
I found that no matter which approach you take, there are three critical components that machines need in order to learn using Deep Learning:
- Neural networks and matrix math
- Backpropagation to learn
- Gradient descent to guide learning
Neural Networks and Matrix Math
Neural networks are a network or circuit of nodes, modeled loosely after the human brain, that are designed to recognize patterns. They interpret labeled input sensory data (e.g., images, photos, handwriting, speech, sound waves, vibration waves, acoustic waves) through machine perception, labeling or clustering of raw input and calculate (score) the results. Neural networks are trained with massive data sets to classify or recognize this labeled sensory data. After that, the neural network is just a simple exercise in Matrix Multiplication (see Figure 2).
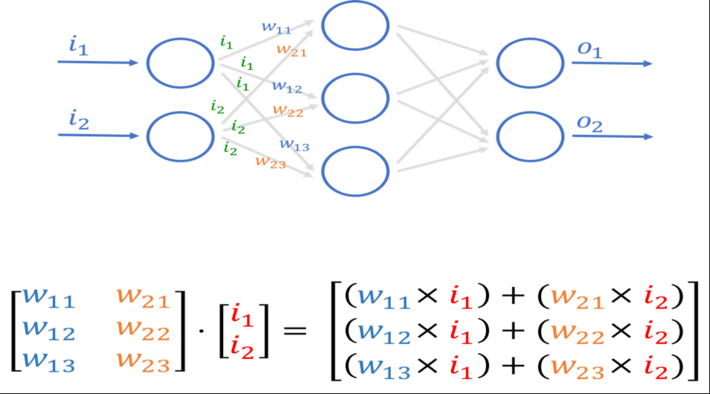
Figure 2: Neural Network and Matrix Multiplication
A neural network is comprised of an Input Layer (where the data gets read and initially processed) and then a number (which can be a large number) of intermediate or hidden layers where the model weights (hyperparameters) are calculated. Finally, the Output Layer contains the results and the score (confidence level) of the results…from input to representation (see Figure 3).
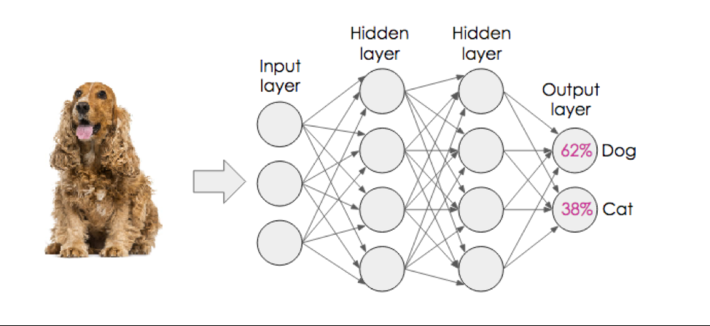Figure 3: Structure of a Neural Network: Input, Hidden and Output Layers
So, now we understand the basics for how neural networks works, but how does the neural network learn? Introducing Backpropagation and Gradient Descent.
Backpropagation to Learn
“The miraculous fact on which the rest of AI stands is that when you have a circuit (neural network) and you impose constraints on your circuits using data, you can find a way to satisfy these constraints by iteratively making small changes to the base of your neural network until its predictions satisfy the data” — Ilya Sutskever, Chief scientist of OpenAI and all round uber smart person.
Notice how the results of Figure 3 are not exact. In fact, there is a high level of error (38% confidence of the dog being recognized as a cat?). It is this error that provides the feedback for the neural network to learn. Each iteration of the neural network and the subsequent evaluation of the expected result versus actual result creates an error that is used to propagate back through the neural network making adjustments to the weights (see Figure 4).
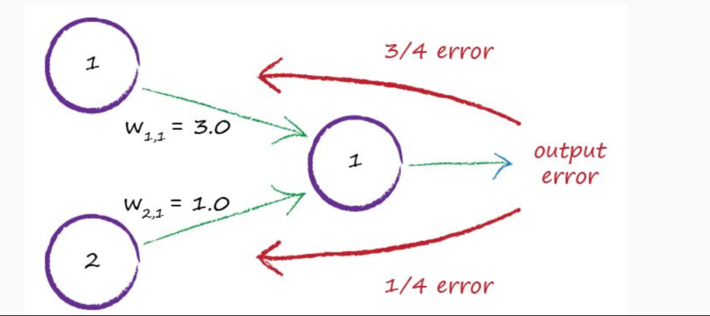
Figure 4: Propagate the output error back to adjust the neural network node weights
Backpropagation (backward propagation) is an important mathematically-based tool for improving the accuracy of predictions of neural networks by gradually adjusting the weights until the expected model results match the actual model results. Backpropagation solves the problem of finding the best weights to deliver the best expected results.
Backpropagation iteratively makes small changes to the weights in the neural networks until the predictions satisfy the data. Backpropagation is a way to find the shortest circuits in deep neural network architectures, where the forward propagation over a number of well-trained connections outputs the right outputs given the inputs.
To guide its learning process, neural networks use backpropagation to compute a gradient descent with respect to the weights and the expected results.
Stochastic Gradient Descent to Guide Learning
Stochastic Gradient Descent is a mathematically-based optimization algorithm (think second derivative in calculus) used to minimize some cost function by iteratively moving in the direction of steepest descent as defined by the negative of the gradient (slope). Gradient descent guides the updates being made to the weights of our neural network model by pushing the errors from the models results back into the weights (see Figure 5).
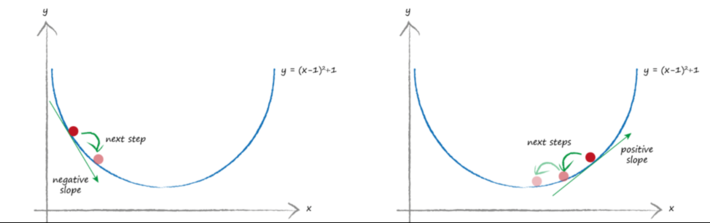
Figure 5: Gradient Descent Leads to Model Optimization
Notice in Figure 5 how in both examples the gradient descent moves you to where the slope of the mathematical equation is equal to zero. With gradient descent, the model continues to tweak the model in order to get to the lowest error value.
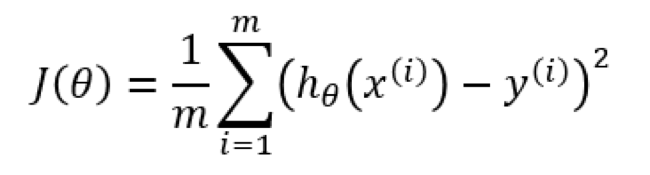
The squaring the error value has the effect of punishing “large” errors and tolerating “small” errors which causes the Stochastic Gradient Descent model to converge more quickly without over-shooting the minimum value (and causing the model to swing back and forth like a pendulum over the lowest value).
In summary, Backpropagation is the process of calculating the partial derivative of the error across the weights of the neural network. Backpropagation gives the amount of change in error with respect to the changes in the weights. The Stochastic Gradient Descent is the optimization process that update those weights in the opposite (Descent part) of the gradient (Derivative).
Neural Networks Assessment
While I am totally amazed at what leading data scientists are doing with neural networks (cancer recognition from x-rays, plant disease recognition from drone photos, natural language process, chatbots, handwriting recognition, facial recognition, sentiment recognition, fraud detection, predictive maintenance, threat detection, etc.), the problems that are being solved today with neural networks are very narrowly focused on specific, well-defined problems of recognition.
And while I am not a data scientist, there seems to be some significant limitations to today’s neural network algorithms including:
- Current deep learning systems seem to be missing a higher layer or level of abstraction that allows the neural network models to generalize. What I mean is that humans are pretty good at seeing and studying a problem, and then making a determination that “this problem looks similar to that problem” and can re-apply learnings from the previous model to the new problem. Building deeper and wider neural networks with uber fast neural network-specific chips isn’t going to solve this abstraction problem.
- Neural networks lack intuition-based exploration and active learning (asking questions and probing provocative ideas) to guide the model learning process. Much of the learning for neural network models are based upon adding a bit of randomness and seeing what happens. Seems that this approach will only yield results that are only marginally different than what the model is already achieving versus exploring entirely new areas.
- Neural network models are very brittle and overly-dependent upon the data in the training data sets. If future data deviates or “drifts” due to changes in the world (economic, technology, social, cultural, etc.), then the neural network model quickly becomes ineffective.
- Finally, the Black Box nature of the neural network results don’t help the business and operational stakeholders to understand cause-and-effect ramifications, which limits the ability of the models to drive actions or recommendations
Maybe the biggest challenge with Neural Networks is that they are based upon deterministic mathematical formulas (matrix algebra, calculus) which works great in a world of deterministic behaviors governed by laws of motion, physics, botany, chemistry, thermodynamics, electrodynamics, metallurgy, etc. Unfortunately, the human mind is not deterministic or even logical or rationale (just visit Las Vegas to see how illogical and irrational the mind works). So, using Neural Networks to replicate human behaviors not only seems impossible, but also seems undesirable. See the blog “Data Analytics and Human Heuristics: How to Avoid Making Poor Decis…” for more insights into the irrational nature of the human mind.
Schmarzo Suggestions
So, what can we do to help neural networks deliver more relevant results? Here are some immediate thoughts (and will build upon these in future blogs):
- Fully understanding expected rewards and penalties requires a substantial investment in time and effort. Organizations need to fully understand the holistic scope of the rewards (business, operational, customer, societal, environmental) as well as the penalties including the costs associated with False Positives and False Negativesas well as potential unintended consequences. If rewards and penalties are too sparse, then effective learning cannot happen.
- Active collaboration across all key stakeholders will be required in defining expected rewards and penalties including the impact of behavioral tendencies such as the Prisoners Dilemma.
- Understand the importance of adopting Design Thinkingtechniques to fuel model discovery and exploration, especially in tapping the heuristics that subject matter experts use today to help accelerate model development and learning vis-à-vis model expected results.
- Embrace the Hypothesis Development Canvasto ensure that the neural network is focused on driving the most relevant operational outcomes.
By the way, I’m happy to announce the release of my 3rd book: “The Art of Thinking Like A Data Scientist”. This book is designed to be a workbook – a pragmatic tool that you can use to help your organization leverage data and analytics to power your business and operational models. The book is jammed with templates, worksheets, examples and hands-on exercises, all composed to help reinforce and deploy the fundamental concepts of “Thinking Like A Data Scientist.”
Advanced Deep Learning Topics
I asked my senior data scientists – Wei and Mauro – to review my blog to make sure that I didn’t say anything too stupid. Boy, was that a mistake. They came back with several additional topics that I should cover, but I’ve decided to make those topics – Universal Approximation Theorem, Recurrent Neural Networks, Feedforward Neural Networks and Activation Function – topics for a future Deep Learning blog.
Video Homework Assignments
These three videos are great for a basic understanding of how neural networks work.
- But what *is* a neural network? | Deep learning, chapter 1
- Gradient descent, how neural networks learn | Deep learning, chapter 2
- What is backpropagation really doing? | Deep learning, chapter 3
