Sometimes you start a blog with a hypothesis in mind, and then that intention changes as you research and realize that your original idea was wrong.  Yep, this is one of those blogs.  Learning can be fun if you let go of pre-existing dogma and learn along your life journey.

I’ve always been curious (a good trait) about economics’ role in developing an organization’s business-driven AI and Data strategies.  And that relationship comes to life when we compare economic value and the AI utility function.

• Economic Value measures the value derived from a good or service to an individual or a company. Economic value can also be the maximum price or amount of money someone is willing to pay for a good or service.
• AI Utility Function is a mathematical function used by AI systems to optimize their decision-making processes based on the desired outcomes of the impacted stakeholders; it defines the goal or goals that the AI is programmed to optimize. The utility function determines the AI model’s actions by evaluating the potential outcomes of different activities and selecting the one that maximizes the expected utility.

The relationship between economic value and the AI utility function lies in that the AI Utility Function is comprised of the utility values of the diverse set of internal and external stakeholders’ desired outcomes (and the KPIs and metrics that measure outcomes effectiveness) to achieve a particular business or operational result.

For example, an AI system designed to make personalized product recommendations could use data on a user’s past purchases and preferences to create a utility function that reflects the user’s economic value for select products or services. The AI model could then optimize its individualized recommendations based on the individual’s economic value, as reflected in the AI Utility Function.

The AI Utility Function assigns values to the AI system’s actions based on the economic value of outcomes. The AI models’ preferences over possible outcomes can be captured by a function that maps these outcomes to a utility value; the higher the number, the more that agent likes that outcome (Figure 1).

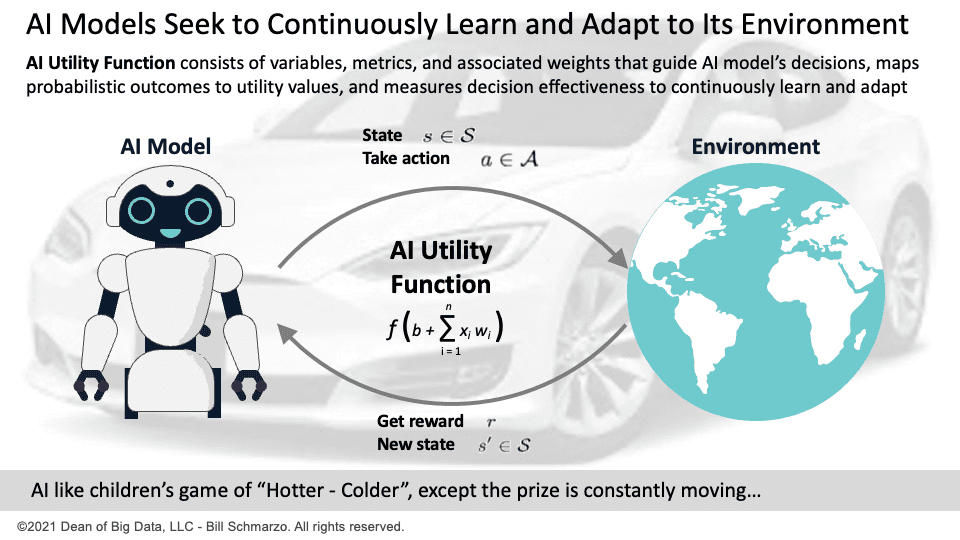
Figure 1: Critical Role of AI Utility Function

AI Utility Function and Stakeholders’ Economic Value

Ideally, the AI Utility Function should align with the economic value of the stakeholders impacted by the AI system. In practice, designing an AI utility function that maximizes the overall utility of all stakeholders is impossible. Different stakeholders may have different preferences, values, goals, and desired outcomes, which may conflict with other stakeholders’ preferences, values, goals, and desired outcomes. For example, an AI system that optimizes environmental sustainability may not be optimal for economic growth.

Therefore, it is essential to carefully consider the different stakeholders’ economic values when designing an AI utility function. This involves understanding the key stakeholders’ preferences, goals, and desired outcomes when constructing the AI Utility Function to balance the trade-offs between conflicting objectives. The conflict in balancing the economic value of the different stakeholders is what leads to a healthy AI Utility Function (Figure 2).

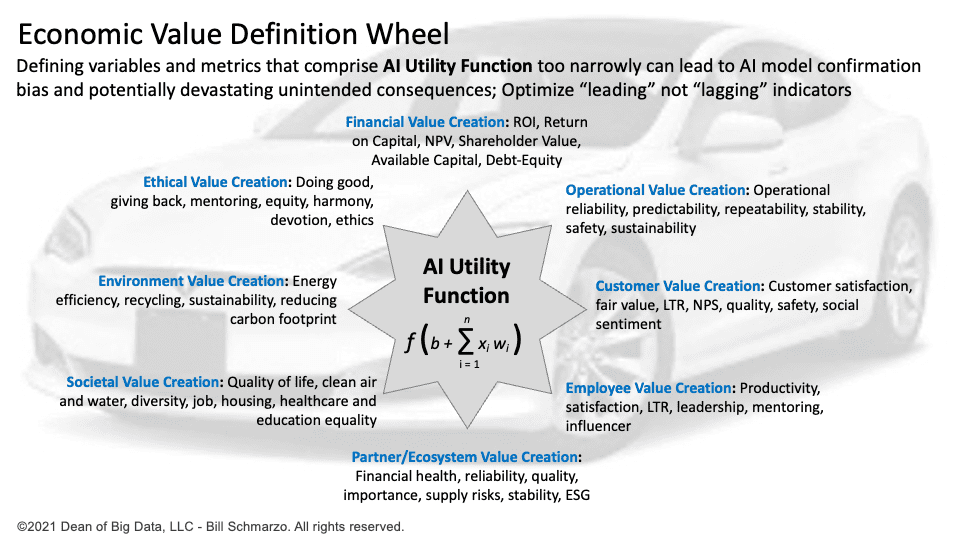
Figure 2: Economic Value Definition Wheel

Incorporating the conflicting utility values of different stakeholders in the AI utility function is vital in constructing a healthy AI model that can adapt and adjust to changing circumstances. The AI system needs to consider different stakeholders’ diverse interests and goals (economic value) and constantly seek to balance the trade-offs between these economic values as the AI model interacts with its operating environment.

AI Utility Function, Multi-objective Optimization, Pareto-optimal Solution…Oh My!

Multi-objective optimization (MOO) is used to optimize problems with multiple objectives, where the goal is to find the best possible solution that simultaneously optimizes multiple conflicting objectives. In MOO, instead of searching for a single optimal solution, the goal is to find a set of solutions that represents the best trade-off between the various objectives.

One way to balance conflicting economic values is using a multi-objective optimization approach (MOO), where the AI system is designed to optimize multiple utility functions simultaneously. Each utility function represents the preferences and goals of a different stakeholder or group of stakeholders. The AI system seeks to find a solution that maximizes the overall utility of all stakeholders while considering the trade-offs between conflicting objectives.

The multi-objective optimization approach can be used to design an AI system that optimizes multiple utility functions simultaneously, such as customer satisfaction, profitability, and environmental sustainability.  Multiple analytic algorithms can be used to optimize multiple objectives or utility functions simultaneously:

• Weighted Sum Method: This simple approach combines multiple objectives into a single objective function by assigning weights to each objective. The objective function is then optimized using traditional optimization techniques.
• Pareto Front Method: This approach involves finding the Pareto front, which is the set of solutions not dominated by any other solution. This can be achieved using mathematical programming techniques such as linear programming or non-linear programming.
• Evolutionary Algorithms: Evolutionary algorithms such as Genetic Algorithm, Particle Swarm Optimization, Differential Evolution, and Multi-Objective Evolutionary Algorithm are commonly used in MOO. These algorithms generate a set of candidate solutions and then use selection, crossover, and mutation operations to evolve a set of solutions that represent the Pareto front.
• Constraint Method: This approach adds constraints to the objective function to ensure that the resulting solution satisfies certain conditions. These constraints can be used to ensure that the solution is feasible and satisfies all the objectives.
• Multi-Objective Linear Programming: In this approach, multiple objectives are represented as linear functions, and the problem is formulated as a linear program. The objective functions are then optimized subject to constraints.
• Multi-Objective Quadratic Programming: This approach is similar to multi-objective linear programming, but the objective functions are represented as quadratic functions.
• Nonlinear Programming: In this approach, the objective functions and constraints are represented as nonlinear functions. Techniques such as gradient-based methods and nonlinear programming solvers can be used to solve the problem.
• Multi-Objective Tabu Search: This stochastic search algorithm uses a tabu list to prevent the search from revisiting solutions that have already been explored. It works by moving through the solution space and swapping variables to explore new regions of the space.

Let’s dive into Pareto-optimal Solutions (because I find the visualizations of the concept easy for me to understand).

Pareto-optimal Solutions

Pareto-optimal solutions are a set of solutions in a multi-objective optimization problem that are not dominated by any other solution in the problem space. In other words, a Pareto-optimal solution is a solution that cannot improve one objective without worsening at least one other objective.

Pareto-optimal solutions represent the best compromise between conflicting objectives. Each Pareto-optimal solution corresponds to a different trade-off between the various objectives. For example, in an AI system designed to optimize customer satisfaction and profitability, a Pareto-optimal solution might represent a trade-off between providing more resources and services to customers (to increase customer satisfaction) and minimizing costs (to increase profitability).

The set of Pareto-optimal solutions is called the Pareto Frontier.  The Pareto Frontier is an essential economic concept in contemplating the optimal outcomes in a given economic system. It provides a framework for analyzing the trade-offs between competing objectives and preferences. The Pareto Frontier can be visualized as a two-dimensional or three-dimensional space, where each point on the curve or surface represents a Pareto-optimal solution (Figure 3).

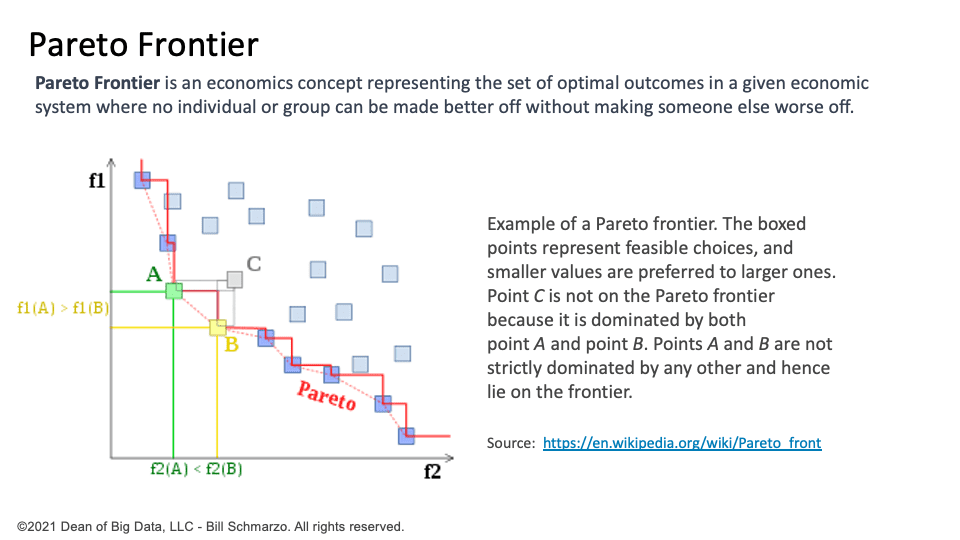
Figure 3: Pareto Frontier

Pareto optimality allows us to find the best compromise between conflicting objectives and make informed decisions based on trade-offs between those conflicting objectives.

Creating a Healthy AI Utility Function Summary

Conflict is good if you want to learn and grow.  Little is gained if everyone thinks the same way and with the same objectives.  But life is about trade-offs, so should it be true for our AI models and the AI Utility Function that guides the AI model’s actions?

Understanding economic value and concepts like multi-objective optimization, Pareto Solutions, and Pareto Frontier enable us to create AI Utility Functions that mirror the real-life struggles of balancing competing yet essential objectives.  That’s an important step in creating healthy AI Utility Functions that guide the AI model’s ability to deliver responsible and ethical outcomes.