Welcome to the series of articles on the secrets of time series modeling. Today’s edition features the nested cross-validation — a lesser-known technique that mitigates some of the fundamental issues with the traditional time series cross-validation.
Why do we need cross-validation in time series modeling?
Time series modeling, compared to traditional nontemporal modeling, presents unique challenges in ensuring that models generalize well to future, unseen data. One key methodology to address these challenges is cross-validation.
Time series data inherently contains temporal dependencies — observations are ordered in time, and future values may depend on past trends. This structure makes it challenging to estimate how well a model will perform on new, unseen data. Cross-validation is important for a few reasons:
- Out-of-sample evaluation provides a robust framework for assessing model performance on data that the model has never seen, reducing the risk of overly optimistic estimates.
- Model Robustness: Cross validation helps verify that the model captures underlying patterns rather than noise by repeatedly training and testing on different segments of the data.
- Temporal Order Preservation: For time series, methods like time series split (which respect the chronological order) are essential to prevent leakage of future information into the training process.
- Hyperparameter Tuning: Reliable performance estimation during hyperparameter optimization ensures that the chosen model configuration generalizes well beyond the training data.
- More Out-of-Sample Data: Cross-validation strategies like walk-forward validation with sliding or expanding windows, allow models to be tested on multiple future periods. This increases the amount of out-of-sample evaluation compared to a single training/validation/test split, offering a more comprehensive view of how performance evolves over time and under varying market conditions.
In summary, proper cross-validation techniques safeguard against overfitting and ensure that time series models remain reliable when deployed in real-world forecasting scenarios, such as quantitative finance and bioinformatics.
Traditional (non-nested) cross-validation: Anchored and unanchored approaches
Traditional cross-validation typically involves splitting the dataset into training and testing subsets. For time series, this can be achieved using two main approaches:
Anchored Cross-Validation
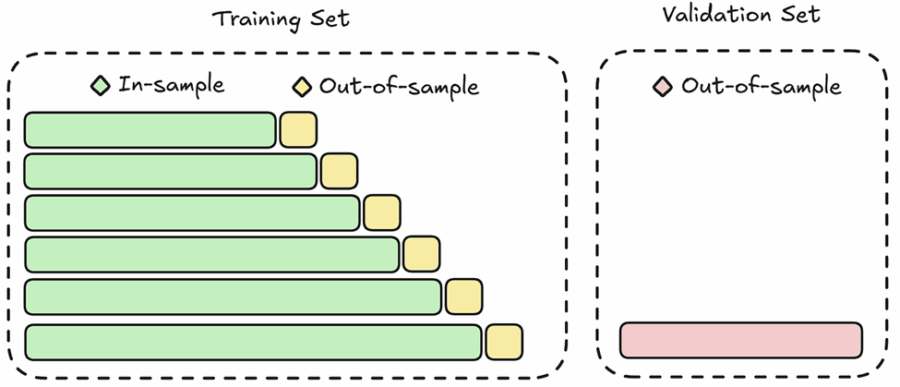
Anchored (Expanding Window) Walk-Forward Cross-Validation
Also known as expanding window validation, anchored CV begins with an initial training period and then progressively expands the training set while moving the testing window forward. It has the advantage of simulating a real-time learning scenario where all past data is used to predict future outcomes. The limitation, however, is that early splits may be based on very limited data, potentially leading to unstable performance estimates.
Unanchored Cross-Validation
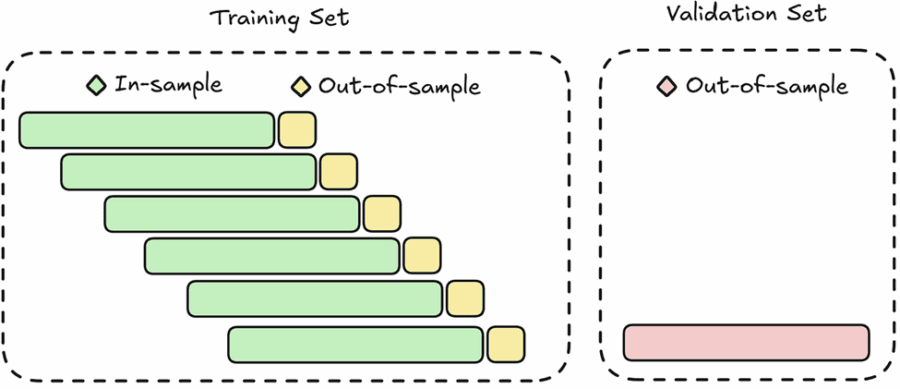
Unanchored (Sliding) Walk-Forward Cross-Validation
This method, also known as sliding window validation, uses fixed-size training and testing windows that move across the dataset without accumulating past data. By maintaining a consistent training size, it can adapt more effectively to recent changes in the data, making it particularly useful in cases where older observations may no longer be informative.
Both anchored and unanchored strategies share a common drawback: they do not decouple the process of model tuning from performance evaluation. When the same data is used to optimize hyperparameters and assess model performance, the risk of data leakage and overfitting increases.
What is nested cross-validation, and what problems does it solve?
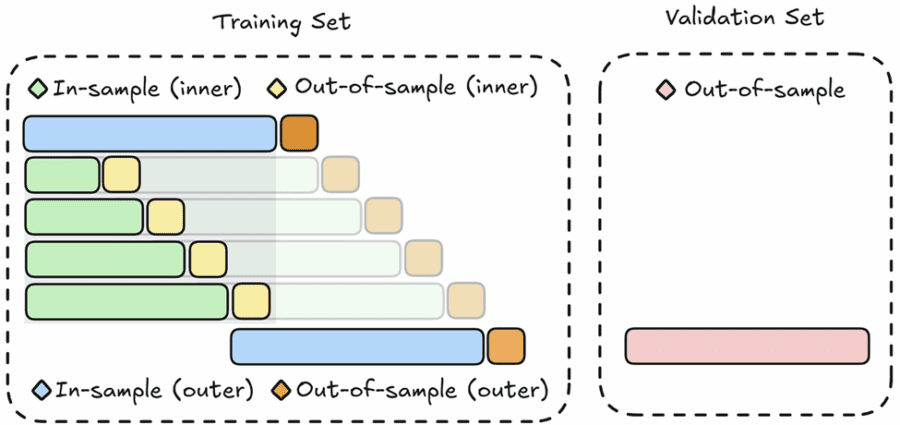
Nested (Anchored Walk-Forward) Cross-Validation
The aim of nested cross-validation is to eliminate the bias in the performance estimate due to the use of cross-validation to tune the hyperparameters. Nested cross-validation addresses the key shortcoming of traditional cross-validation by separating hyperparameter tuning from the performance evaluation process. It involves two loops:
- Inner Loop: Used exclusively for hyperparameter optimization. Here, techniques like grid search identify the best parameters by further splitting the training data into smaller in-sample and out-of-sample subsets.
- Outer Loop: Used to assess the generalization performance of the model with its optimized hyperparameters. The model is trained on the training set (with the best parameters found in the inner loop) and evaluated on the holdout validation set.
This hierarchical structure ensures that:
- No Information Leakage Occurs: The evaluation in the outer loop remains unbiased since it never sees data that was used for hyperparameter tuning.
- Unbiased Error Estimation: It provides an unbiased estimate of the model’s ability to generalize, which is critical when models require extensive tuning.
- Reduced Overfitting Risk: By separating model selection from performance evaluation, nested CV minimizes the chance of overfitting to the dataset’s particular quirks.
Why should you use nested cross-validation?
There is a significant amount of evidence that Nested Cross Validation improves the performance of the resulting model.
Bias reduction
A study published by Tougui et al. (2021) compared several cross-validation methods across common predictive modeling tasks. The findings indicated that nested cross-validation reduced optimistic bias by approximately 1% to 2% for the area under the receiver operating characteristic curve (AUROC) and 5% to 9% for the area under the precision-recall curve (AUPR). In contrast, non-nested methods exhibited higher levels of optimistic bias, suggesting that nested CV provides more reliable performance estimates. Comparative study in healthcare predictive modeling by Wilimitis et al. (2023) reinforces that nested CV systematically yields lower (and more realistic) performance estimates than non‐nested approaches.
Unbiased error estimation
Additional research by Bates et al. (2023), Vabalas et al. (2019), and Krstajic et al. (2014) has demonstrated that nested CV offers unbiased estimates of out-of-sample error, even for datasets comprising only a few hundred samples. This advantage is crucial for building robust predictive models, as it ensures that the model’s performance is a true reflection of its ability to generalize. Reviews in the literature, such as the paper by Varma and Simon (2006) emphasize that isolating the tuning process via nested CV prevents data leakage, thereby yielding performance estimates that closely match the error on completely unseen data.
Overfitting mitigation
A study by Ghasemzadeh et al. (2024) focusing on machine learning models in speech, language, and hearing sciences found that nested CV provided the highest statistical confidence and power while yielding an unbiased accuracy estimate. Remarkably, the necessary sample size with a single holdout could be up to 50% higher compared to what would be needed using nested CV. Confidence in the model based on nested CV was up to four times higher than in the single holdout-based model. Additional studies show that when hyperparameter tuning is separated into an inner loop (as in nested CV), the risk of overfitting is significantly reduced. For example, Cawley and Talbot (2010) showed that nested cross‐validation yields nearly unbiased error estimates by isolating the hyperparameter search, thereby reducing the chance of selecting models that perform well only on the training/tuning data.
These papers highlight that while nested cross-validation is computationally more intensive, its benefits in providing reliable, unbiased performance estimates far outweigh the additional cost, particularly in settings with limited data or complex hyperparameter tuning.
How does nested cross-validation reduce overfitting?
Empirical studies and theoretical insights both highlight nested cross-validation as a powerful tool for reducing overfitting. But what exactly makes it so effective?
Separation of duties
As previously mentioned, nested cross-validation clearly distinguishes between model tuning and performance evaluation. The inner loop is dedicated solely to hyperparameter tuning and model selection, while the outer loop assesses the model’s performance on unseen data. This separation prevents the tuning process from biasing the final performance estimates.
Robust generalization
By employing multiple in-sample and out-of-sample splits in the outer loop, nested cross-validation averages out the inconsistencies of any single data partition. This averaging process results in a more stable and reliable estimate of how the model will perform in real-world scenarios.
Prevention of data leakage
The inherent design of nested cross-validation ensures that no information from the tuning phase contaminates the evaluation phase. This strict isolation between the two stages directly mitigates the risk of overfitting, providing a more accurate reflection of the model’s true predictive power.
Implementation
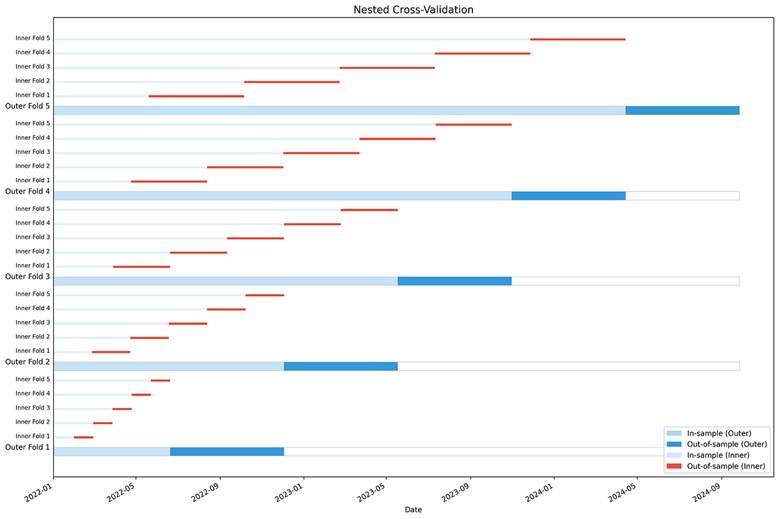
This is a very rudimentary implementation of the nested cross-validation framework, but it should give you a good starting point:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
from typing import Callable, Any, Optional
from matplotlib.patches import Patch
import matplotlib.dates as mdates
class NCVEngine:
def __init__(
self,
outer_splits: int = 5,
inner_splits: int = 3,
):
self.outer_splits = outer_splits
self.inner_splits = inner_splits
self.outer_cv = TimeSeriesSplit(n_splits=outer_splits)
self.results = {}
self.df = None
self.X = None
self.y = None
self.target_col = None
def _run_cv(
self,
cv,
X: np.ndarray,
y: np.ndarray,
train_func: Callable,
test_func: Callable,
extra_keys: Optional[dict] = None,
) -> list[dict]:
results = []
for i, (train_idx, test_idx) in enumerate(cv.split(X)):
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
model = train_func(X_train, y_train)
metrics = test_func(model, X_test, y_test)
result = {
"fold": i,
"model": model,
"metrics": metrics,
"train_idx": train_idx,
"test_idx": test_idx,
"train_size": len(X_train),
"test_size": len(X_test),
}
if extra_keys:
result.update(extra_keys)
results.append(result)
return results
def process_inner_folds(
self,
X_train: np.ndarray,
y_train: np.ndarray,
outer_fold: int,
) -> dict:
inner_cv = TimeSeriesSplit(n_splits=self.inner_splits)
inner_results = self._run_cv(
inner_cv,
X_train,
y_train,
self.inner_train,
self.inner_test,
extra_keys={"outer_fold": outer_fold},
)
best_model = min(inner_results, key=lambda r: r["metrics"]["mse"])[
"model"
]
return {"all_results": inner_results, "best_model": best_model}
def process_outer_folds(
self,
X: np.ndarray,
y: np.ndarray,
) -> dict:
outer_results = []
for i, (train_idx, test_idx) in enumerate(self.outer_cv.split(X)):
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
inner_results = self.process_inner_folds(X_train, y_train, i)
final_model = self.outer_train(X_train, y_train)
test_metrics = self.outer_test(final_model, X_test, y_test)
outer_results.append(
{
"fold": i,
"train_idx": train_idx,
"test_idx": test_idx,
"train_size": len(X_train),
"test_size": len(X_test),
"inner_results": inner_results,
"final_model": final_model,
"test_metrics": test_metrics,
}
)
avg_metrics = {
"mse": np.mean([r["test_metrics"]["mse"] for r in outer_results]),
"r2": np.mean([r["test_metrics"]["r2"] for r in outer_results]),
}
return {"outer_results": outer_results, "average_metrics": avg_metrics}
def process_folds(
self,
df: pd.DataFrame,
target_col: str,
) -> dict:
self.df = df
self.target_col = target_col
self.X = df.drop(columns=[target_col]).values
self.y = df[target_col].values
self.results = self.process_outer_folds(self.X, self.y)
return self.results
def plot_folds(self) -> None:
if not self.results or self.df is None or self.df.empty:
raise ValueError("No results available. Run process_folds first.")
fig, ax = plt.subplots(figsize=(15, 10))
date_nums = mdates.date2num(self.df.index.to_pydatetime())
start_date = date_nums[0]
end_date = date_nums[-1] + 1
outer_train_color = "#AED6F1"
outer_test_color = "#3498DB"
inner_train_color = "#D6EAF8"
inner_val_color = "#E74C3C"
outer_height = 0.6
inner_height = 0.15
y_space = 1.0
outer_results = self.results.get("outer_results", [])
for i, outer_fold in enumerate(outer_results):
y_pos = i * (self.inner_splits + 1) * y_space
train_idx = outer_fold["train_idx"]
test_idx = outer_fold["test_idx"]
ax.barh(
y_pos,
width=end_date - start_date,
height=outer_height,
left=start_date,
color="white",
alpha=0.3,
edgecolor="gray",
)
for idx in train_idx:
ax.barh(
y_pos,
width=1,
height=outer_height,
left=date_nums[idx],
color=outer_train_color,
alpha=0.7,
)
for idx in test_idx:
ax.barh(
y_pos,
width=1,
height=outer_height,
left=date_nums[idx],
color=outer_test_color,
)
ax.text(
start_date - 5,
y_pos + outer_height / 2,
f"Outer Fold {i + 1}",
ha="right",
va="center",
fontsize=10,
)
inner_results = outer_fold["inner_results"]["all_results"]
for j, inner_fold in enumerate(inner_results):
inner_y_pos = y_pos + (j + 1) * y_space
inner_train_idx = inner_fold["train_idx"]
inner_test_idx = inner_fold["test_idx"]
for idx in inner_train_idx:
ax.barh(
inner_y_pos,
width=1,
height=inner_height,
left=date_nums[idx],
color=inner_train_color,
alpha=0.7,
)
for idx in inner_test_idx:
ax.barh(
inner_y_pos,
width=1,
height=inner_height,
left=date_nums[idx],
color=inner_val_color,
)
ax.text(
start_date - 5,
inner_y_pos + inner_height / 2,
f"Inner Fold {j + 1}",
ha="right",
va="center",
fontsize=8,
)
ax.set_xlabel("Date")
ax.set_title("Nested Cross-Validation", fontsize=14)
ax.xaxis_date()
date_formatter = mdates.DateFormatter("%Y-%m")
ax.xaxis.set_major_formatter(date_formatter)
fig.autofmt_xdate()
legend_elements = [
Patch(facecolor=outer_train_color, label="In-sample (Outer)"),
Patch(facecolor=outer_test_color, label="Out-of-sample (Outer)"),
Patch(facecolor=inner_train_color, label="In-sample (Inner)"),
Patch(facecolor=inner_val_color, label="Out-of-sample (Inner)"),
]
ax.legend(handles=legend_elements, loc="lower right")
ax.set_yticks([])
plt.tight_layout()
def inner_train(
self,
X: np.ndarray,
y: np.ndarray,
) -> Any:
raise NotImplementedError("Subclasses must implement inner_train")
def inner_test(
self,
model: Any,
X: np.ndarray,
y: np.ndarray,
) -> dict:
raise NotImplementedError("Subclasses must implement inner_test")
def outer_train(
self,
X: np.ndarray,
y: np.ndarray,
) -> Any:
raise NotImplementedError("Subclasses must implement outer_train")
def outer_test(
self,
model: Any,
X: np.ndarray,
y: np.ndarray,
) -> dict:
raise NotImplementedError("Subclasses must implement outer_test")
class NCVExample(NCVEngine):
def inner_train(
self,
X: np.ndarray,
y: np.ndarray,
) -> Lasso:
model = Lasso(fit_intercept=False)
model.fit(X, y)
return model
def inner_test(
self,
model: Lasso,
X: np.ndarray,
y: np.ndarray,
) -> dict:
y_pred = model.predict(X)
return {
"mse": mean_squared_error(y, y_pred),
"r2": r2_score(y, y_pred),
"predictions": y_pred,
}
def outer_train(
self,
X: np.ndarray,
y: np.ndarray,
) -> Lasso:
return self.inner_train(X, y)
def outer_test(
self,
model: Lasso,
X: np.ndarray,
y: np.ndarray,
) -> dict:
return self.inner_test(model, X, y)
def summarize_results(self) -> None:
if not self.results:
raise ValueError("No results available. Run process_folds first.")
print("=" * 50)
print("NESTED CROSS-VALIDATION RESULTS")
print("=" * 50)
print(f"Average MSE: {self.results['average_metrics']['mse']:.4f}")
print(f"Average R²: {self.results['average_metrics']['r2']:.4f}")
print("-" * 50)
for i, fold in enumerate(self.results["outer_results"]):
print(f"Outer Fold {i + 1}:")
print(
f" Train size: {fold['train_size']},"
)
print(
f" Test size: {fold['test_size']}"
)
print(
f" Test MSE: {fold['test_metrics']['mse']:.4f}, ",
f"R-squared: {fold['test_metrics']['r2']:.4f}",
)
inner_mses = [
r["metrics"]["mse"]
for r in fold["inner_results"]["all_results"]
]
print(
" Inner validation MSEs: "
+ ", ".join([f"{mse:.4f}" for mse in inner_mses])
)
print(f" Avg inner validation MSE: {np.mean(inner_mses):.4f}")
print("-" * 50)
def generate_synthetic_timeseries(
n_samples: int = 100,
n_features: int = 3,
noise_level: float = 0.5,
trend_strength: float = 0.1,
seasonality: bool = True,
) -> pd.DataFrame:
time_idx = np.arange(n_samples)
features = np.array(
[
np.random.normal(0, 1, n_samples)
+ trend_strength * time_idx * (i + 1)
+ (
2 * np.sin(2 * np.pi * time_idx / (10 + i * 5))
if seasonality
else 0
)
for i in range(n_features)
]
).T
coefficients = np.random.uniform(
-2,
2,
n_features,
)
target = np.dot(features, coefficients) + np.random.normal(
0,
noise_level,
n_samples,
)
df = pd.DataFrame(
features,
columns=[f"feature_{i}" for i in range(n_features)],
)
df["target"] = target
df.index = pd.date_range(
start="2000-01-01",
periods=n_samples,
freq="D",
)
return df
# Set random seed for reproducibility
np.random.seed(42)
# Generate synthetic time series data
df = generate_synthetic_timeseries(
n_samples=1000,
n_features=3,
)
# Create and run nested cross-validation
ncv = NCVExample(
outer_splits=5,
inner_splits=5,
)
results = ncv.process_folds(
df,
target_col="target",
)
# Print summary of results
ncv.summarize_results()
# Plot the nested cross-validation structure
ncv.plot_folds()
plt.show()
The end
Nested cross-validation represents a significant advancement over traditional cross-validation methods, particularly in the context of time series modeling, where maintaining the integrity of temporal order is critical. By effectively segregating the hyperparameter tuning process from model evaluation, nested CV delivers unbiased performance estimates, reduces overfitting, and ultimately leads to more robust models.
Although it comes with increased computational costs, the benefits of nested cross-validation, in terms of reliable model evaluation and generalization performance, make it an invaluable tool for predictive modeling. Whether you are working with financial time series, climate data, or biomedical signals, incorporating nested cross-validation into your workflow can enhance the credibility and reliability of your forecasting models.
