There’s plenty of disagreement about the value of economics research. Skeptics say that economists have predicted eight of the last five recessions, or zero of them. Economists and their fans point to supposed economic achievements such as stable, low inflation and (often) steady growth. In this blog post I’ll use simple data science techniques to attempt to measure progress in economics research.
There are many potential ways to measure progress in research. For example, since each published academic paper ostensibly makes a contribution to a field, counting the number of published papers in a field could measure that field’s progress. However, this method would overestimate progress if the bulk of published papers drew incorrect conclusions or restated previously established truths. Indeed, a field could conceivably regress rather than progress over time if its practitioners were publishing mostly incorrect conclusions. Other proxies for research progress, for example funding levels or number of practitioners or students, fail for similar reasons.
I think that the proper measure of scientific achievement is predictive accuracy. One reason I believe this is that Albert Einstein believed it. After outlining the theory of general relativity, he was willing to put it to an empirical test, and allowed Sir Arthur Eddington and others to measure the bending of light during a solar eclipse to determine whether Einstein’s predictions were better than those implied by Newton’s physical laws. After they measured the bent light and compared notes, it turned out that Einstein’s model had better predictive accuracy than Newton’s, and thereafter Einstein’s general relativity was broadly accepted. This increase in predictive accuracy was the contribution of Einstein’s theory – not its complexiy, beauty, chronological order, mathematical sophistication, or anything else. After all, the complexity or elegance of a scientific theory mean little if the theory cannot accurately predict reality.
In the spirit of Arthur Eddington measuring starlight during an eclipse, I (or rather the Federal Reserve) measured quarterly unemployment and nominal GDP going back several decades. Then, I compared observed economic realities to the predictions that economists made about them a year beforehand. The Philadelphia Federal Reserve Bank has recorded almost 7,000 individual predictions about unemployment and nominal GDP since the fourth quarter of 1968 and makes these predictions freely downloadable on their website. The important question is: has predictive accuracy improved in economics since 1968? Whether or not there has been an Einstein to revolutionize economic models in the last few decades, we may expect that incremental improvements over the decades have improved predictive accuracy bit by bit. Has this been the case?
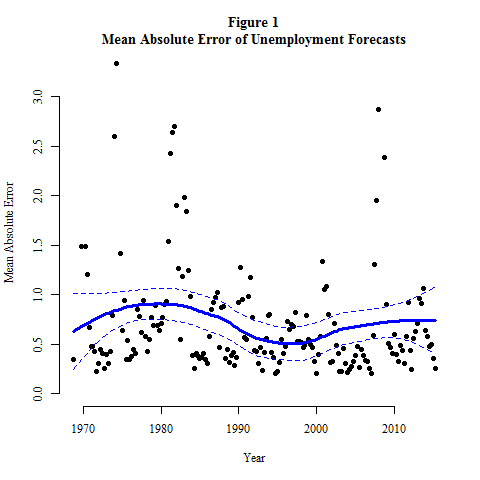
Figure 1, below, shows the mean absolute error of unemployment forecasts since Q4, 1968. To calculate these, I took the absolute value of the difference between predicted and actual unemployment rates for each individual forecast, then I took the mean of these differences for each quarter. Figure 1 also shows a loess line with its 95% confidence interval going through the graphed points. Figure 1 doesn’t look good for economics: the loess line hits its lowest point in the mid 1990’s (just like pop music did), and the loess predicted value for 1968 is about the same as for 2015, with very similar confidence intervals as well. There is little or no evidence for improved predicted accuracy here, and thus (I argue) little or no evidence for progress in economics.
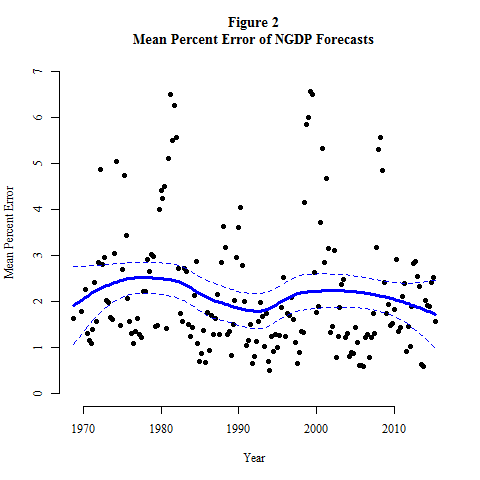
Figure 2 shows the analogous trend for predictions of nominal GDP. Here, I calculated mean percent error rather than mean absolute error to avoid the constant growth of GDP distorting the measurement of errors. Just like in Figure 1, the errors were calculated for each of the nearly 7,000 individual forecasts and then averaged by quarter, with a loess line and confidence interval added afterwards. Here the results look a little better for economics: the minimum value of the predicted loess value is reached at the most recent quarter in the dataset, and certainly since 2000 the trend looks like it’s generally downward. However I am not convinced; the confidence interval of the loess curve has changed very little over the decades and I do not believe there is much evidence here either for progress in economics.
I am a skeptic and a pessimist about progress in economics research. However, there are several reasons why reasonable people may disagree with me. For example, people might disagree with my local regression methodology, or they might point out that Figure 2 really does provide evidence for progress that I am wrongly dismissing, or they might have other arguments. I will not attempt to refute every counterargument here, and if critics would like, please get in touch with me and I would be happy to share my data with you so that you can perform and publish your own analysis.
My final, skeptical point, is that even if we optimistically assume that economics research is progressing, and will continue to progress indefinitely, that progress could take a form that makes progress essentially pointless anyway. In Figure 3, Panel A, I imagine two scenarios that show predictive accuracy improving over time. Over a short time horizon, they appear similar, and even if economics is indeed progressing, I submit that it is not clear which scenario we are living in (or which our world most closely resembles).
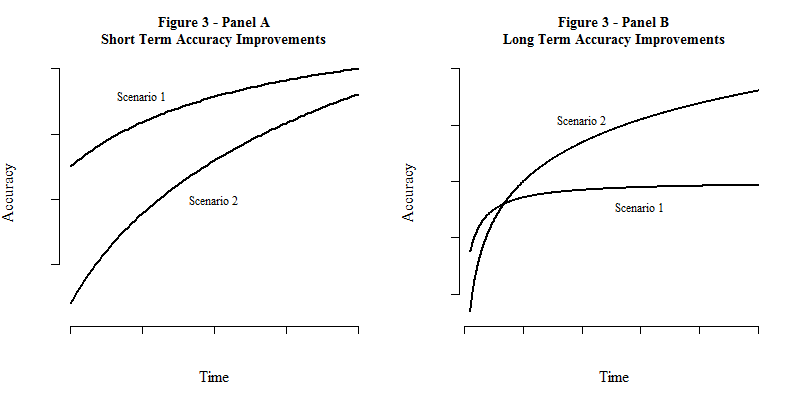
Figure 3, Panel B, shows the exact same curves that are plotted in Panel A, but over a longer time horizon. This makes the difference between the two scenarios more apparent. Scenario 2 is actually a logarithmic curve, which grows slowly but diverges to infinity. Scenario 1 is a curve with an upper asymptote, and even though it is monotonically increasing, it will never exceed that upper horizontal asymptote. We could be living in Scenario 2, where growing computational power and unceasing incremental breakthroughs will improve the predictive accuracy of economics beyond any conceivable limit. But we could also be in Scenario 1, where irreducible complexity in our social systems, or upper limits of computational power, or fundamental randomness in the universe mean that we can never exceed a certain level of predictive accuracy.
I wonder what economics will look like in a thousand years. If we recreate Figures 1 and 2 in the year 3016, will the loess line continue to hover where it is now? Will our prediction errors slowly sink towards 0 as economic science gradually perfects itself? Or will its progress peter out at some intermediate value, as humanity pushes the upper limit of predictive accuracy in economics? If we are pushing towards a limit like in Scenario 1 of Figure 3, is it worth pushing? Should we continue to spend millions on research funding and waste wood pulp (or hard drive space) publishing papers that could not possibly yield much improvement in our predictions of reality? If not, should we shut down all the journals and abolish research professorships after we are “done” progressing (for example, by being within 1% of the upper asymptote of accuracy)?
These are hard questions for several reasons, but I think they are not asked enough. For economics, and for data science, and for every other scientific pursuit, I think we should have a sense of the long game. We should ask ourselves: what is the goal of the next thousand years of economics, or of data science? Or, indeed, of psychology, or physics? I think that the goal must have something to do with creating simple, broadly applicable models that improve predictive accuracy in real situations. After knowing our goals, we should strive to get a sense of whether we are achieving them. In this post, I’ve showed a little bit of data that (I think) indicates that we are not making progress towards the goals of economics. I hope that people who agree as well as those who disagree will join and sharpen the conversation about progress in economics and science in general. I look forward to reading and hearing what you think.
(This post was originally written for bradfordtuckfield.com.)