This article is from Win-Vector LLC
In this article we will discuss the machine learning method called “decision trees”, moving quickly over the usual “how decision trees work” and spending time on “why decision trees work.” We will write from a computational learning theory perspective, and hope this helps make both decision trees and computational learning theory more comprehensible. The goal of this article is to set up terminology so we can state in one or two sentences why decision trees tend to work well in practice.
Introduction
Newcomers to data science are often disappointed to learn that the job of the data scientist isn’t tweaking and inventing new machine learning algorithms.
In the “big data” world supervised learning has been a solved problem since at least 1951. Some reasons this isn’t as well known as one would expect include:
- Statisticians (the writers of the mentioned references) use different terminology than computer scientists (the typical current audience). Essentially any time you see a statistician use terms like “consistent”, “efficient”, or “asymptotic” you need to check if they are talking about provably optimal estimation procedures.
- “Big data” didn’t arrive until much later, so we have to wait for and many others to re-observe that supervised machine learning is easy whey you have a lot of data.
- Prospective machine learning tinkerers do not want this to be true. They seem to hope to have the pleasure of getting paid to use their programming chops to re-implement all of machine learning from scratch in their favorite language.
Decision Trees obviously continued to improve after [GordonOlshen1978]. For example: CART’s cross-validation and pruning ideas (see: [BreimanEtAl1984]). Working on the shortcomings of tree-based methods (undesirable bias, instability) led to some of the most important innovations in machine learning (bagging and boosting, for example see: [HastieTibshiraniFriedman2009]).
In [ZumelMount2014] we have a section on decision trees (section 6.3.2) but we restrict ourselves to how they work (and the consequences), how to work with them; but not why they work. The reason we did not discuss why they work is the process of data science, where practical, includes using already implemented and proven data manipulation, machine learning, and statistical methods. The “why” can be properly delegated to implementers. Delegation is part of being a data scientist, so you have to learn to trust delegation at some point.
However, we do enjoy working through the theory and exploring why different machine learning algorithms work (for example our write-up on support vector machines: how they work here Mount2011, and why they work here Mount2015).
In this note we will look at the “why” of decision trees. You may want work through a decision tree tutorial to get the “what” and “how” out of the way before reading on (example tutorial: [Moore]).
Decision Trees
Decision trees are a type of recursive partitioning algorithm. Decision trees are built up of two types of nodes: decision nodes, and leaves. The decision tree starts with a node called the root. If the root is a leaf then the decision tree is trivial or degenerate and the same classification is made for all data. For decision nodes we examine a single variable and move to another node based on the outcome of a comparison. The recursion is repeated until we reach a leaf node. At a leaf node we return the majority value of training data routed to the leaf node as a classification decision, or return the mean-value of outcomes as a regression estimate. The theory of decision trees is presented in Section 9.2 of [HastieTibshiraniFriedman2009].
Figure 6.2 from Practical Data Science with R ([ZumelMount2014]) below shows a decision tree that estimates the probability of an account cancellation by testing variable values in sequence (moving down and left or down and right depending on the outcome). For true conditions we move down and left, for falsified conditions we move down and right. The leaves are labeled with the predicted probability of account cancellation. The tree is orderly and all nodes are in estimated probability units because Practical Data Science with R used a technique similar to y-aware scaling ([Zumel2016]).
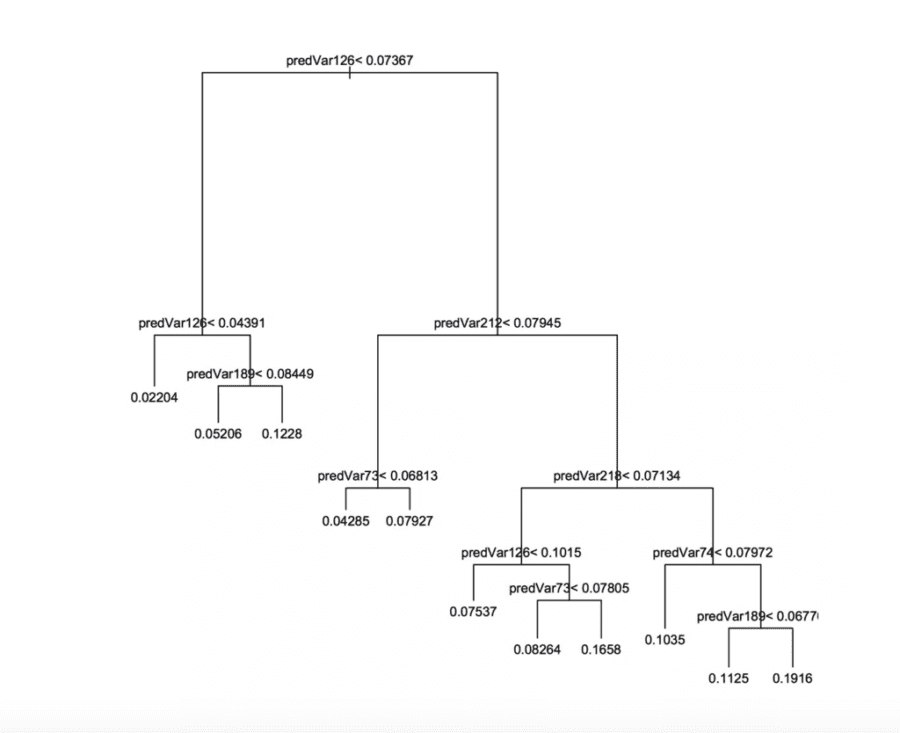
Graphical representation of a decision tree
It isn’t too hard to believe that a sufficiently complicated tree can memorize training data. Decision tree learning algorithms have a long history and a lot of theory in how they pick which variable to split and where to split it. The issue for us is: will the produced tree work about as well on future test or application data as it did on training data?
To read the full original article (and to learn about computational learning theory, fitting the data and over-fit avoidance, with source code) click here. For more decision tree related articles on DSC click here.
DSC Resources
- Services: Hire a Data Scientist | Search DSC | Classifieds | Find a Job
- Contributors: Post a Blog | Ask a Question
- Follow us: @DataScienceCtrl | @AnalyticBridge
Popular Articles
